====================================================================


Maple

==================================================================== 

Maple é uma ferramenta de computação científica com as seguintes características gerais:

° Manipulador Simbólico

° Grande coleção de Funções Numéricas

° Capacidade gráfica em 2D e 3D

° Linguagem de programação avançada

° Sintaxes similar ao FORTRAN, PASCAL ou C

° Folha de Cálculo e Editor de Texto com saídas em Latex e HTML

° Maple está disponível para DOS, Windows, MacOS, UNIX, Linux...
° A grande vantagem : uma folha de cálculo pode ser utilizada sobre qualquer plataforma sem necessidade de ser alterada.

>   

1_Sintaxes_Básica

2 Primeiros Passos

3 Cálculo Elementar

4 Resolução de sistemas de equações algébricas

5 Equações Diferenciais 

6 Manipulação Algébrica

7 Bibliotecas

8 Gráficos e Visualização

9 Aplicações

10 Processos em UNIX
11 Maple e Latex





====================================================================

   1  Sintaxes Básica:

  1.-    Zona de Texto (Em cor preta)

 2.-    Zona de comandos (Em cor vermelha)  (Cada comando debe finalizar com    ;    o com  :   )

 3.-  Zona de respostas (Em cor Azul)

>   

25! + 13^23;

57265115456744102351045797

  as líneas com comentários se colocam a continuação do  símbolo  #

>   

c^2  =  a^2 + b^2 ; # Teorema de Pitágoras

c^2 = a^2+b^2

O seguinte comando reinicia a folha de cálculo

>   

restart;

>   


====================================================================

   2  Primeiros Passos

Maple faz cálculos tanto com números inteiros como   em Ponto Flutuante

>   

15 + 5^20;

95367431640640

>   

15. + 5^20;

.9536743164e14

Porém a ênfase radica nos cálculos  exatos

>   

cos(Pi/12)^2 + ln(2/3+5)/7;

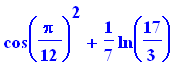
cos(1/12*Pi)^2+1/7*ln(17/3)

>   

evalf(%); # EVALuate using Floating-point

1.180812853

A % pode ser utilizado a última saída de Maple  como entrada não comando seguinte.

Existe mais ordem de precedência para os  operadores:   + -  * /  ^

>   

1+2*3^2;

19

>   

(1+2)*3^2;

27

Porém, seu uso descuidado produz erros  

>   

2^3^5; 

Error, `^` unexpected

>   

(2^3)^5;

32768

>   

2^-5; 

Error, `-` unexpected

>   

2^(-5);

1/32

Constantes numéricas e letras gregas:   Maple  faz distinção  entre maiúsculas e minúsculas

>   

evalf(Pi);

3.141592654

>   

evalf(pi);

pi

A precisão pode ser  controlada:

>   

sqrt( 68 ); sqrt( 68. ); evalf(sqrt(68),50 );

2*17^(1/2)

8.246211251

8.2462112512353210996428197119481540502943984507472

Se pode arredondar a uma fração

>   

convert(%,fraction);

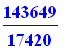
143649/17420

 o simbolo %  permite que a ultima saída se assine a uma nova instrução!

>   

restart;

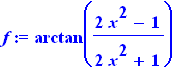
Para atribuir um objeto a uma variável se faz com o operador  :=

>   

f := arctan( (2*x^2-1)/(2*x^2+1) );

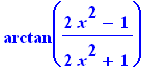
f := arctan((2*x^2-1)/(2*x^2+1))

>   

f;

arctan((2*x^2-1)/(2*x^2+1))

Entretanto que o símbolo  = ,  se utiliza para mostrar uma relação entre variáveis

>   

h = x + y;

h = x+y

>   

h;

h

 Por lo tanto, existem nomes que já estão definidos  e por lo tanto não podes ser utilizados

>   

abs:= f*sin(x); 

Error, attempting to assign to `abs` which is protected

abs  é a função valor absoluto

>   

abs(x-a);

abs(x-a)

>   

restart;

====================================================================

   3  Cálculo Elemental

Se definem, se avaliam e se derivam funções  abstratas

>   

f:= (x,y) -> exp(x^2+y^2)/(x-y);

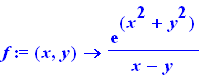
f := proc (x, y) options operator, arrow; exp(x^2+y^2)/(x-y) end proc

>   

f(a^(1/2),b^(1/2));

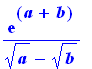
exp(a+b)/(a^(1/2)-b^(1/2))

>   

f(2,3);

-exp(13)

>   

evalf(%);

-442413.3920

>   

diff( f(x,y) , x) + diff( f(x,y) , y) ;

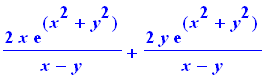
2*x*exp(x^2+y^2)/(x-y)+2*y*exp(x^2+y^2)/(x-y)

Conserva as expressões para a derivada  interna

>   

f:= (t,r) -> g(c*t+r) + h(c*t-r);

f := proc (t, r) options operator, arrow; g(c*t+r)+h(c*t-r) end proc

>   

diff(f(t,r),t$3);

`@@`(D,3)(g)(c*t+r)*c^3+`@@`(D,3)(h)(c*t-r)*c^3

Para funções compostas se utiliza o operador @ e para derivar o operador   D

>   

(cos@ln@sqrt)(x);

cos(ln(x^(1/2)))

>   

D(cos@ln@sqrt)(x);

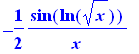
-1/2*sin(ln(x^(1/2)))/x

>   

diff(cos(ln(sqrt(x))),x);

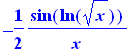
-1/2*sin(ln(x^(1/2)))/x

  Limites:

>   

f:= (x) -> 1/(1+r/x)^x;

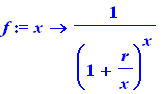
f := proc (x) options operator, arrow; 1/((1+r/x)^x) end proc

>   

Limit(f(x),x=infinity) = limit(f(x), x=infinity);

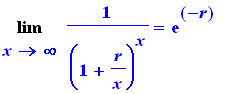
Limit(1/((1+r/x)^x),x = infinity) = exp(-r)

As maiúsculas a a esquerda (  Limit  ) fornecem uma representação do  Limite. as minúsculas ( limit  ) sua execução.

Também podemos calcular limites a esquerda e a direita.

>   

g:= (x)-> tan(x + Pi) ;

g := proc (x) options operator, arrow; tan(x+Pi) end proc

>   

Limit(g(x), x=Pi/2,right)=limit(g(x),x=Pi/2,right);

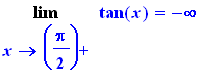
Limit(tan(x),x = 1/2*Pi,right) = -infinity

Somatórios

>   

Sum((1+i)/i^2, i = 1..n) ;

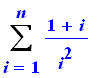
Sum((1+i)/i^2,i = 1 .. n)

>   

value(%);

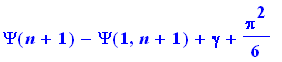
Psi(n+1)-Psi(1,n+1)+gamma+1/6*Pi^2

Se tiver dúvidas

>   

?gamma

>   

?Psi

Integração:

>   

g:=(x)-> 1/( x*( b*x+c*x^2)^(1/2) );

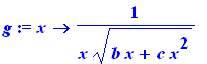
g := proc (x) options operator, arrow; 1/(x*(b*x+c*x^2)^(1/2)) end proc

>   

Int( g(x) , x ) = int( g(x) , x );

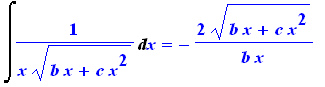
Int(1/(x*(b*x+c*x^2)^(1/2)),x) = -2/b/x*(b*x+c*x^2)^(1/2)

  Avalia integrais definidas tanto analítica como numericamente

>   

f:=(x)->  exp(Pi*x);

f := proc (x) options operator, arrow; exp(Pi*x) end proc

>   

Int( f(x) , x=1..3) = int( f(x) , x=1..3);

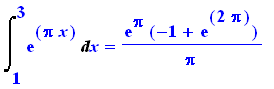
Int(exp(Pi*x),x = 1 .. 3) = exp(Pi)*(-1+exp(2*Pi))/Pi

Avalia integrais impróprias e as funções que resultam

>   

h:= (t)-> exp(-t)*t^(z-1);

h := proc (t) options operator, arrow; exp(-t)*t^(z-1) end proc

>   

Int(h(t),t=0..infinity) = int(h(t),t=0..infinity);

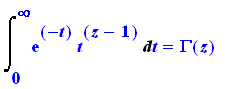
Int(exp(-t)*t^(z-1),t = 0 .. infinity) = GAMMA(z)

>   

?GAMMA

>   

GAMMA(0.5); # Função Gamma

1.772453851

>   

Int(x/(x^2+2*x+2),x) = int(x/(x^2+2*x+2),x);

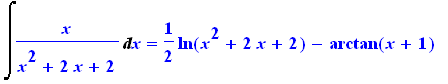
Int(x/(x^2+2*x+2),x) = 1/2*ln(x^2+2*x+2)-arctan(x+1)

Comprovemos que a  solução é a correta

>   

diff(rhs(%),x);

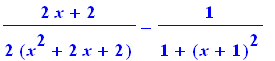
1/2*(2*x+2)/(x^2+2*x+2)-1/(1+(x+1)^2)

>   

simplify(%);

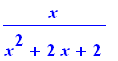
x/(x^2+2*x+2)

>   

restart;

====================================================================

   4  Resolução de sistemas de equações Algébricas

Resolve sistemas de equações algébricas.  O resultado fica armazenado em uma lista, e logo se deve atribuir esses valores ao  "nome" das variáveis correspondentes para seguir operando.

>   

ecu1:= R[1]*i[1]+R[3]*i[3]+R[4]*i[4]-V[1]=0;

ecu1 := R[1]*i[1]+R[3]*i[3]+R[4]*i[4]-V[1] = 0

>   

ecu2:= R[2]*i[2]-V[2]-R[3]*i[3]=0;

ecu2 := R[2]*i[2]-V[2]-R[3]*i[3] = 0

>   

ecu3:=  i[1]-i[2]-i[3]= 0;

ecu3 := i[1]-i[2]-i[3] = 0

>   

solve({ecu1,ecu2,ecu3},{i[1],i[2],i[3]} ); assign(%);

{i[1] = -(-V[2]*R[3]+R[3]*R[4]*i[4]-R[3]*V[1]+R[2]*R[4]*i[4]-R[2]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3]), i[3] = -1/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])*(R[1]*V[2]+R[2]*R[4]*i[4]-R[2]*V[1]), i[2] = (R[1]*V[2...
{i[1] = -(-V[2]*R[3]+R[3]*R[4]*i[4]-R[3]*V[1]+R[2]*R[4]*i[4]-R[2]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3]), i[3] = -1/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])*(R[1]*V[2]+R[2]*R[4]*i[4]-R[2]*V[1]), i[2] = (R[1]*V[2...

>   

i[1],i[2],i[3];

-(-V[2]*R[3]+R[3]*R[4]*i[4]-R[3]*V[1]+R[2]*R[4]*i[4]-R[2]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3]), (R[1]*V[2]+V[2]*R[3]-R[3]*R[4]*i[4]+R[3]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3]), -1/(R[2]*R[1]+R[2]*R[3]+...

Agora para avaliar  x, y, z nas  equações   ecu1 ... ecu3

>   

ecu1; ecu2; ecu3;

-R[1]*(-V[2]*R[3]+R[3]*R[4]*i[4]-R[3]*V[1]+R[2]*R[4]*i[4]-R[2]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])-R[3]/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])*(R[1]*V[2]+R[2]*R[4]*i[4]-R[2]*V[1])+R[4]*i[4]-V[1] = 0

R[2]*(R[1]*V[2]+V[2]*R[3]-R[3]*R[4]*i[4]+R[3]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])-V[2]+R[3]/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])*(R[1]*V[2]+R[2]*R[4]*i[4]-R[2]*V[1]) = 0

-(-V[2]*R[3]+R[3]*R[4]*i[4]-R[3]*V[1]+R[2]*R[4]*i[4]-R[2]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])-(R[1]*V[2]+V[2]*R[3]-R[3]*R[4]*i[4]+R[3]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])+1/(R[2]*R[1]+R[2]*R[3]+R[1...
-(-V[2]*R[3]+R[3]*R[4]*i[4]-R[3]*V[1]+R[2]*R[4]*i[4]-R[2]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])-(R[1]*V[2]+V[2]*R[3]-R[3]*R[4]*i[4]+R[3]*V[1])/(R[2]*R[1]+R[2]*R[3]+R[1]*R[3])+1/(R[2]*R[1]+R[2]*R[3]+R[1...

>   

simplify(ecu1); simplify(ecu2); simplify(ecu3);

0 = 0

0 = 0

0 = 0

Seguidamente procedemos a "limpar"o conteúdo das variáveis  para poder utilizá-las em outras expressões.

>   

i[1]:='i[1]';  i[2]:='i[2]';  i[3]:='i[3]';

i[1] := 'i[1]'

i[2] := 'i[2]'

i[3] := 'i[3]'

Soluções aproximadas para encontrar as raízes de um polinômio

>   

p:= x^3 - 3*x^2 = 17*x - 51;

p := x^3-3*x^2 = 17*x-51

>   

sol:=solve(p,x);

sol := 3, 17^(1/2), -17^(1/2)

>   

evalf(%);

3., 4.123105626, -4.123105626

>   

q:= x^5 +3*x^4 - 6*x^3 + x^2 + 12*x - 14=0;

q := x^5+3*x^4-6*x^3+x^2+12*x-14 = 0

>   

solve(q , x);

RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 1), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 2), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 3), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index...
RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 1), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 2), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 3), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index...
RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 1), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 2), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 3), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index...
RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 1), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 2), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 3), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index...
RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 1), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 2), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index = 3), RootOf(_Z^5+3*_Z^4-6*_Z^3+_Z^2+12*_Z-14,index...

>   

?RootOf

>   

fsolve(q,x); # fsolve utiliza Ponto-flotante

-4.264823400, -1.539657626, 1.190651733

>   

restart:

====================================================================

   5  Equações Diferenciais

>   

ED1:=diff(y(x),x)+y(x)/x=alpha/(x*y(x)^2);

ED1 := diff(y(x),x)+y(x)/x = alpha/x/y(x)^2

>   

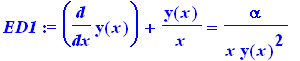
dsolve(ED1,y(x));

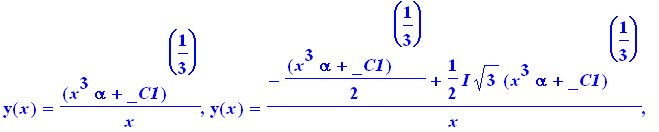
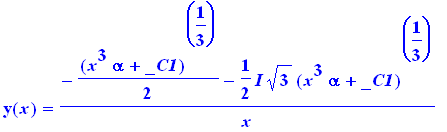
y(x) = (x^3*alpha+_C1)^(1/3)/x, y(x) = (-1/2*(x^3*alpha+_C1)^(1/3)+1/2*I*3^(1/2)*(x^3*alpha+_C1)^(1/3))/x, y(x) = (-1/2*(x^3*alpha+_C1)^(1/3)-1/2*I*3^(1/2)*(x^3*alpha+_C1)^(1/3))/x
y(x) = (x^3*alpha+_C1)^(1/3)/x, y(x) = (-1/2*(x^3*alpha+_C1)^(1/3)+1/2*I*3^(1/2)*(x^3*alpha+_C1)^(1/3))/x, y(x) = (-1/2*(x^3*alpha+_C1)^(1/3)-1/2*I*3^(1/2)*(x^3*alpha+_C1)^(1/3))/x

>   

sols:=dsolve({ED1,y(1)=5},y(x));

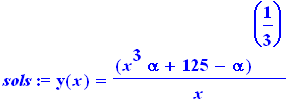
sols := y(x) = (x^3*alpha+125-alpha)^(1/3)/x

Resolve equações diferencias, com e sem valores inicias por vários métodos. Séries . . .

>   

dsolve({ED1,y(1)=5},y(x),series);

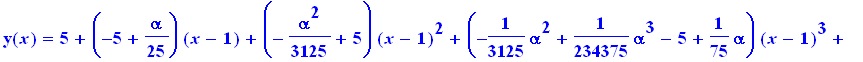
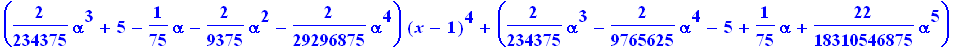
y(x) = series(5+(-5+1/25*alpha)*(x-1)+(-1/3125*alpha^2+5)*(x-1)^2+(-1/3125*alpha^2+1/234375*alpha^3-5+1/75*alpha)*(x-1)^3+(2/234375*alpha^3+5-1/75*alpha-2/9375*alpha^2-2/29296875*alpha^4)*(x-1)^4+(2/23...
y(x) = series(5+(-5+1/25*alpha)*(x-1)+(-1/3125*alpha^2+5)*(x-1)^2+(-1/3125*alpha^2+1/234375*alpha^3-5+1/75*alpha)*(x-1)^3+(2/234375*alpha^3+5-1/75*alpha-2/9375*alpha^2-2/29296875*alpha^4)*(x-1)^4+(2/23...
y(x) = series(5+(-5+1/25*alpha)*(x-1)+(-1/3125*alpha^2+5)*(x-1)^2+(-1/3125*alpha^2+1/234375*alpha^3-5+1/75*alpha)*(x-1)^3+(2/234375*alpha^3+5-1/75*alpha-2/9375*alpha^2-2/29296875*alpha^4)*(x-1)^4+(2/23...

Sistemas de equações Diferencias. Mediante transformações de Laplace. . .

>   

sys:= diff(y(x),x)=z(x) , diff(z(x),x)=y(x);

sys := diff(y(x),x) = z(x), diff(z(x),x) = y(x)

>   

fcns:={y(x),z(x)};

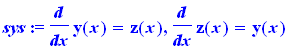
fcns := {y(x), z(x)}

>   

s:=dsolve({sys,y(0)=0,z(0)=1},fcns,method=laplace);

s := {z(x) = cosh(x), y(x) = sinh(x)}

>   

s[1]; # Selecçãoo uma de as soluções

z(x) = cosh(x)

Podemos tomar unicamente o lado direito da  solução para uma posterior  manipulação

>   

2*( rhs(s[1] )); # right hand sides

2*cosh(x)

  equações diferenciais famosas:   Bessel

>   

ED2:=x^2*diff(y(x),x$2)+x*diff(y(x),x)+(x^2-mu)*y(x)=0;

ED2 := x^2*diff(y(x),`$`(x,2))+x*diff(y(x),x)+(x^2-mu)*y(x) = 0

>   

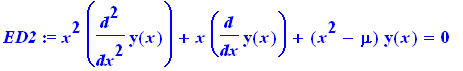
dsolve(ED2,y(x)); assign(%);

y(x) = _C1*BesselJ(mu^(1/2),x)+_C2*BesselY(mu^(1/2),x)

>   

simplify(ED2);

0 = 0

Se  podem fazer gráficas para um conjunto de  condições  inicias

>   

y:=subs(mu=10, _C1=1/2, _C2=1/3 ,y(x));

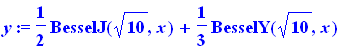
y := 1/2*BesselJ(10^(1/2),x)+1/3*BesselY(10^(1/2),x)

>   

plot(y, x=0..20,-2..1 ,title=`y(x)`);

[Maple Plot]

Soluções Numéricas:

>   

de1 :={diff(g(t),t$2)=-f(t)-g(t),diff(f(t),t$2)= diff(g(t),t)+f(t)};

de1 := {diff(g(t),`$`(t,2)) = -f(t)-g(t), diff(f(t),`$`(t,2)) = diff(g(t),t)+f(t)}

>   

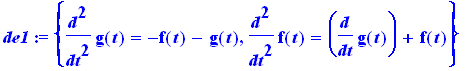
init1 := {g(0)=1, D(g)(0)=0, f(0)=0, D(f)(0)=1}:

>   

F := dsolve(de1 union init1, {g(t),f(t)},type=numeric);

F := proc (x_rkf45) local res, data, vars, solnproc, outpoint, ndsol, i; option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _En...

>   

F(0.0);

[t = 0., f(t) = 0., diff(f(t),t) = 1., g(t) = 1., diff(g(t),t) = 0.]

>   

F:=dsolve(de1 union init1,{g(t),f(t)},type=numeric,output=array([0,1,2,3,4]));

F := matrix([[vector([t, f(t), diff(f(t),t), g(t), diff(g(t),t)])], [matrix([[0., 0., 1., 1., 0.], [1., .966818091329165741, .876014924666769668, .382939951992786132, -1.29441467524315002], [2., 1.6139...

>   

with(plots): 

Warning, the name changecoords has been redefined

>   

odeplot(F,[t,g(t)],1..10,labels=[t,g]);

[Maple Plot]

>   

odeplot(F,[t,f(t)],1..10,labels=[t,f]);

[Maple Plot]

>   

with(DEtools):

>   

S:=cos(xi)*diff(h(xi),xi$3)-diff(h(xi),xi$2)+Pi*diff(h(xi),xi)=h(xi)-xi;

S := cos(xi)*diff(h(xi),`$`(xi,3))-diff(h(xi),`$`(xi,2))+Pi*diff(h(xi),xi) = h(xi)-xi

>   

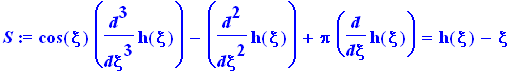
DEplot(S,h(xi),xi=-2.5..1.4,[[h(0)=1,D(h)(0)=2,(D@@2)(h)(0)=1]],h=-4..5,stepsize=.05);

[Maple Plot]

>   

restart;

====================================================================

   6  Manipulação Algébrica

Maple ,  automaticamente avalia e simplifica expressões

>   

p:=(a+b)^3*(a+b)^2;

p := (a+b)^5

>   

expand(p);

a^5+5*a^4*b+10*a^3*b^2+10*a^2*b^3+5*a*b^4+b^5

>   

factor(p);

(a+b)^5

>   

t:=cos(x)^5+sin(x)^4+2*cos(x)^2-2*sin(x)^2-cos(2*x);

t := cos(x)^5+sin(x)^4+2*cos(x)^2-2*sin(x)^2-cos(2*x)

>   

simplify(t);

cos(x)^4*(cos(x)+1)

>   

r:=alpha*(x^3-y^3)/(beta*(x^2+x-y-y^2));

r := alpha*(x^3-y^3)/beta/(x^2+x-y-y^2)

>   

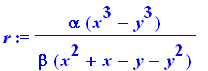
normal(r);

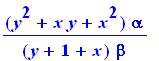
(y^2+x*y+x^2)*alpha/(y+1+x)/beta

>   

n:=numer(r); d:=denom(r);

n := alpha*(-x^3+y^3)

d := beta*(-x^2-x+y+y^2)

>   

n*d*delta;

alpha*(-x^3+y^3)*beta*(-x^2-x+y+y^2)*delta

>   

expand(%);

alpha*beta*delta*x^5+alpha*beta*delta*x^4-alpha*beta*delta*x^3*y-alpha*beta*delta*x^3*y^2-alpha*beta*delta*y^3*x^2-alpha*beta*delta*y^3*x+alpha*beta*delta*y^4+alpha*beta*delta*y^5

>   

collect(%,x);

alpha*beta*delta*x^5+alpha*beta*delta*x^4+(-alpha*beta*delta*y-alpha*beta*delta*y^2)*x^3-alpha*beta*delta*y^3*x^2-alpha*beta*delta*y^3*x+alpha*beta*delta*y^4+alpha*beta*delta*y^5

>   

coeff(%,x^3);

-alpha*beta*delta*y-alpha*beta*delta*y^2

>   

factor(%);

-y*alpha*beta*delta*(1+y)

pode converter muitos tipos de expressões em outras mais especificas

>   

expr1:=(a*x^2+b)/(x*(-3*x^2-x+4));

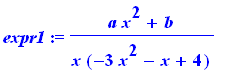
expr1 := (a*x^2+b)/x/(-3*x^2-x+4)

>   

expr2:=convert(expr1,parfrac,x);

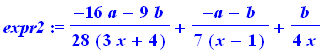
expr2 := 1/28*(-16*a-9*b)/(3*x+4)+1/7*(-a-b)/(x-1)+1/4*b/x

>   

expr3:=sin(x)*cos(x);

expr3 := sin(x)*cos(x)

>   

expr4:=convert(%,exp);

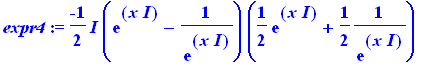
expr4 := -1/2*I*(exp(x*I)-1/exp(x*I))*(1/2*exp(x*I)+1/2*1/exp(x*I))

Se podem isolar os argumentos das expressões

>   

op(3,expr2); op(3,expr4);

1/4*b/x

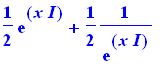
1/2*exp(x*I)+1/2*1/exp(x*I)

>   

op(3,expr2)*op(3,expr4);

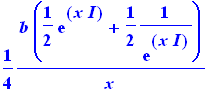
1/4*b/x*(1/2*exp(x*I)+1/2*1/exp(x*I))

>   

simplify(%);

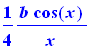
1/4*b/x*cos(x)

Não sempre todo funciona da maneira correta. a seguinte integral é trivial, Porém vejamos lo que sucede com Maple

>   

Int(2*x*(x^2+1)^24,x);

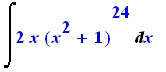
Int(2*x*(x^2+1)^24,x)

>   

value(%);

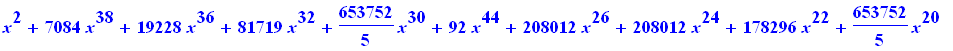
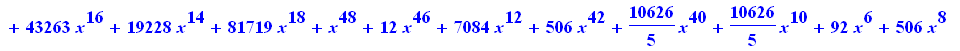
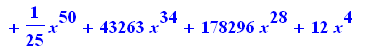
x^2+7084*x^38+19228*x^36+81719*x^32+653752/5*x^30+92*x^44+208012*x^26+208012*x^24+178296*x^22+653752/5*x^20+43263*x^16+19228*x^14+81719*x^18+x^48+12*x^46+7084*x^12+506*x^42+10626/5*x^40+10626/5*x^10+92...
x^2+7084*x^38+19228*x^36+81719*x^32+653752/5*x^30+92*x^44+208012*x^26+208012*x^24+178296*x^22+653752/5*x^20+43263*x^16+19228*x^14+81719*x^18+x^48+12*x^46+7084*x^12+506*x^42+10626/5*x^40+10626/5*x^10+92...
x^2+7084*x^38+19228*x^36+81719*x^32+653752/5*x^30+92*x^44+208012*x^26+208012*x^24+178296*x^22+653752/5*x^20+43263*x^16+19228*x^14+81719*x^18+x^48+12*x^46+7084*x^12+506*x^42+10626/5*x^40+10626/5*x^10+92...

>   

factor(%);

1/25*x^2*(x^8+5*x^6+10*x^4+10*x^2+5)*(x^40+20*x^38+190*x^36+1140*x^34+4845*x^32+15505*x^30+38775*x^28+77625*x^26+126425*x^24+169325*x^22+187760*x^20+172975*x^18+132450*x^16+84075*x^14+43975*x^12+18760*...
1/25*x^2*(x^8+5*x^6+10*x^4+10*x^2+5)*(x^40+20*x^38+190*x^36+1140*x^34+4845*x^32+15505*x^30+38775*x^28+77625*x^26+126425*x^24+169325*x^22+187760*x^20+172975*x^18+132450*x^16+84075*x^14+43975*x^12+18760*...
1/25*x^2*(x^8+5*x^6+10*x^4+10*x^2+5)*(x^40+20*x^38+190*x^36+1140*x^34+4845*x^32+15505*x^30+38775*x^28+77625*x^26+126425*x^24+169325*x^22+187760*x^20+172975*x^18+132450*x^16+84075*x^14+43975*x^12+18760*...

>   

factor(%+1/25);

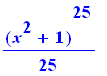
1/25*(x^2+1)^25

>   

restart;

====================================================================

   7  Bibliotecas

No todos os comandos são carregados na memoria quando Maple é iniciado. Só os comandos padrão são carregados automaticamente

>   

P:=  x^5-24*x^4+85*x^3-108*x^2+166*x-120 ;

P := x^5-24*x^4+85*x^3-108*x^2+166*x-120

>   

factor(P);

(x-20)*(x-1)*(x-3)*(x^2+2)

>   

realroot(P);

[[0, 2], [2, 4], [16, 32]]

>   

readlib(realroot):

>   

realroot(P,1);

[[1, 1], [3, 3], [20, 20]]

As Bibliotecas de Maple :

   -   a biblioteca padrão

  - a biblioteca de miscelâneas

  - Paquetes

>   

?index

>   

?index,packages

>   

?index,misc

>   

restart:

====================================================================

   8  Gráficos e Visualização

Una maior capacidade gráfica é obtida como paquete plots

>   

with(plots); 

Warning, the name changecoords has been redefined

[animate, animate3d, animatecurve, arrow, changecoords, complexplot, complexplot3d, conformal, conformal3d, contourplot, contourplot3d, coordplot, coordplot3d, cylinderplot, densityplot, display, displ...
[animate, animate3d, animatecurve, arrow, changecoords, complexplot, complexplot3d, conformal, conformal3d, contourplot, contourplot3d, coordplot, coordplot3d, cylinderplot, densityplot, display, displ...
[animate, animate3d, animatecurve, arrow, changecoords, complexplot, complexplot3d, conformal, conformal3d, contourplot, contourplot3d, coordplot, coordplot3d, cylinderplot, densityplot, display, displ...
[animate, animate3d, animatecurve, arrow, changecoords, complexplot, complexplot3d, conformal, conformal3d, contourplot, contourplot3d, coordplot, coordplot3d, cylinderplot, densityplot, display, displ...
[animate, animate3d, animatecurve, arrow, changecoords, complexplot, complexplot3d, conformal, conformal3d, contourplot, contourplot3d, coordplot, coordplot3d, cylinderplot, densityplot, display, displ...
[animate, animate3d, animatecurve, arrow, changecoords, complexplot, complexplot3d, conformal, conformal3d, contourplot, contourplot3d, coordplot, coordplot3d, cylinderplot, densityplot, display, displ...

  Gráficos básicos em 2 e 3 Dimensões:

>   

f:=x-> exp(-x^2)*sin(Pi*x^3);

f := proc (x) options operator, arrow; exp(-x^2)*sin(Pi*x^3) end proc

>   

plot( f(x),x=-2..2,title=`f(x)`);

[Maple Plot]

>   


>   

g:=(x,y)-> f(x)*f(y);

g := proc (x, y) options operator, arrow; f(x)*f(y) end proc

>   

plot3d(g(x,y),x=-1..1,y=-1..1);

[Maple Plot]

>   


>   

h:=(x) -> cos(sqrt(x^2+3*y^2))/(1+x^2/8);

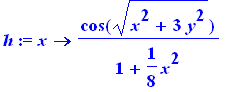
h := proc (x) options operator, arrow; cos(sqrt(x^2+3*y^2))/(1+1/8*x^2) end proc

>   

j:= (x) -> 1/3 -(2*x^2+y^2)/19;

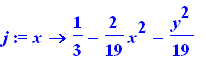
j := proc (x) options operator, arrow; 1/3-2/19*x^2-1/19*y^2 end proc

>   

plot3d({h(x),j(x)},x=-3..3,y=-3..3,title=`Intersecção de h(x) e j(x)`);

[Maple Plot]

Mapas Topológicos

>   

with(plots):

>   

contourplot(sin(x*y),x=-10..10,y=-10..10);

[Maple Plot]

Graficando Campos Vetoriais :

>   

phi[1]:=(x,y)->ln((x^2+2*x+1+y^2)^(1/2));

phi[1] := proc (x, y) options operator, arrow; ln((x^2+2*x+1+y^2)^(1/2)) end proc

>   

phi[2]:=(x,y)->-ln((x^2-2*x+1+y^2)^(1/2));

phi[2] := proc (x, y) options operator, arrow; -ln((x^2-2*x+1+y^2)^(1/2)) end proc

>   

fieldplot([phi[1](x,y),phi[2](x,y)],x=-2..2,y=-2..2,arrows=SLIM,grid=[8,8]);

[Maple Plot]

>   

gradplot((-phi[1](x,y)-phi[2](x,y)),x=-2..2,y=-1..1,arrows=SLIM,grid=[10,10]);

[Maple Plot]

Animações:

>   

animate3d(cos(sqrt(t*x^2+t*y^2)),x=-5..5,y=-5..5,t=1..8);

[Maple Plot]

Com um pouco mais de complexidade

>   

tubeplot({[10*cos(t),10*sin(t),0,t=0..2*Pi,radius=2+cos(7*t),numpoints=120,tubepoint=24],[0,10+5*cos(t),5*sin(t),t=0..2*Pi,radius=1.5,numpoint=50,tubepoint=18]});

[Maple Plot]

>   


====================================================================

   9  Aplicações

  Álgebra Linear

>   

restart:

>   

with(linalg):# Leemoso paquete de A.L. 

Warning, the protected names norm and trace have been redefined and unprotected

>   


Criando Matrizes  e  Vetores

>   

A:=array( [ [a, b, c], [d, e, f ], [g, h, i ] ] );

A := matrix([[a, b, c], [d, e, f], [g, h, i]])

>   

B:=array(antisymmetric,1..3,1..3):

>   

B[1,2]:=x+a; B[1,3]:=y+b; B[2,3]:=z+c;

B[1,2] := x+a

B[1,3] := y+b

B[2,3] := z+c

>   

print(B);

matrix([[0, x+a, y+b], [-x-a, 0, z+c], [-y-b, -z-c, 0]])

>   

v:= vector([1,2,3] );

v := vector([1, 2, 3])

>   

C:=matrix(4,4, (i,j) -> i^(j-1));

C := matrix([[1, 1, 1, 1], [1, 2, 4, 8], [1, 3, 9, 27], [1, 4, 16, 64]])

>   

M:=array(antisymmetric,1..3,1..3):

>   

entermatrix(M);

enter element 1,2 >   

2*alpha;

2*alpha

>   

2*beta;

2*beta

>   

2*gamma:

>   

N:=diag(mu,nu,lambda);

N := matrix([[mu, 0, 0], [0, nu, 0], [0, 0, lambda]])

>   

G:=diag(M,N);

G := matrix([[0, 2*alpha, 2*beta, 0, 0, 0], [-2*alpha, 0, 2*gamma, 0, 0, 0], [-2*beta, -2*gamma, 0, 0, 0, 0], [0, 0, 0, mu, 0, 0], [0, 0, 0, 0, nu, 0], [0, 0, 0, 0, 0, lambda]])

>   


  a função "solve" para resolver um sistema  de  equações:

>   

ec1:= (c^2-1)*x+(c-1)*y = (1-c)^2 ;

ec1 := (c^2-1)*x+(c-1)*y = (1-c)^2

>   

ec2:=(c-1)*x+(c^2-1)*y=c-1;

ec2 := (c-1)*x+(c^2-1)*y = c-1

>   

sis:=({ec1,ec2}):

>   

solve(sis,{x,y});

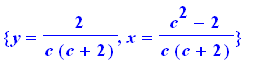
{y = 2/c/(c+2), x = (c^2-2)/c/(c+2)}

>   


Álgebra de matrizes para resolver o sistema  de equações

>   

H:=genmatrix(sis,[x,y],'flag');

H := matrix([[c^2-1, c-1, (1-c)^2], [c-1, c^2-1, c-1]])

>   

A:=genmatrix(sis,[x,y]);

A := matrix([[c^2-1, c-1], [c-1, c^2-1]])

>   

B:=delcols(H,1..2);

B := matrix([[(1-c)^2], [c-1]])

  para resolver a equação A X = B

>   

sol:= linsolve(A,B);

sol := matrix([[(c^2-2)/c/(c+2)], [2/c/(c+2)]])

>   

x:=sol[1,1]; y:=sol[2,1];

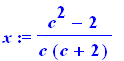
x := (c^2-2)/c/(c+2)

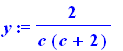
y := 2/c/(c+2)

>   

simplify(ec1); simplify(ec2);

1-2*c+c^2 = (c-1)^2

c-1 = c-1

>   

x:='x': y:='y': # Limpo as variáveis x e

>   


Operações com matrizes

>   

S:=evalm(M+N);

S := matrix([[mu, 2*alpha, 2*beta], [-2*alpha, nu, 2*gamma], [-2*beta, -2*gamma, lambda]])

>   

evalm(3*M + 5/3*N);

matrix([[5/3*mu, 6*alpha, 6*beta], [-6*alpha, 5/3*nu, 6*gamma], [-6*beta, -6*gamma, 5/3*lambda]])

>   

evalm(M*N); 

Error, (in evalm/evaluate) use the &* operator for matrix/vector multiplication

>   

evalm(M &* N);

matrix([[0, 2*alpha*nu, 2*beta*lambda], [-2*alpha*mu, 0, 2*gamma*lambda], [-2*beta*mu, -2*gamma*nu, 0]])

>   

evalm(N &* M);

matrix([[0, 2*alpha*mu, 2*beta*mu], [-2*alpha*nu, 0, 2*gamma*nu], [-2*beta*lambda, -2*gamma*lambda, 0]])

>   

V:= vector([x,y,z]);

V := vector([x, y, z])

>   

evalm(M &* V);

vector([2*alpha*y+2*beta*z, -2*alpha*x+2*gamma*z, -2*beta*x-2*gamma*y])

>   

S1:= evalm( (M)^(3) );

S1 := matrix([[0, 2*(-4*alpha^2-4*beta^2)*alpha-8*alpha*gamma^2, 2*(-4*alpha^2-4*beta^2)*beta-8*beta*gamma^2], [-2*(-4*alpha^2-4*gamma^2)*alpha+8*alpha*beta^2, 0, -8*beta^2*gamma+2*(-4*alpha^2-4*gamma^...

>   

S1:= map(factor,S1);

S1 := matrix([[0, -8*alpha*(alpha^2+beta^2+gamma^2), -8*beta*(alpha^2+beta^2+gamma^2)], [8*alpha*(alpha^2+beta^2+gamma^2), 0, -8*gamma*(alpha^2+beta^2+gamma^2)], [8*beta*(alpha^2+beta^2+gamma^2), 8*gam...

>   

print(S);

matrix([[mu, 2*alpha, 2*beta], [-2*alpha, nu, 2*gamma], [-2*beta, -2*gamma, lambda]])

>   

zeta:=inverse(S);

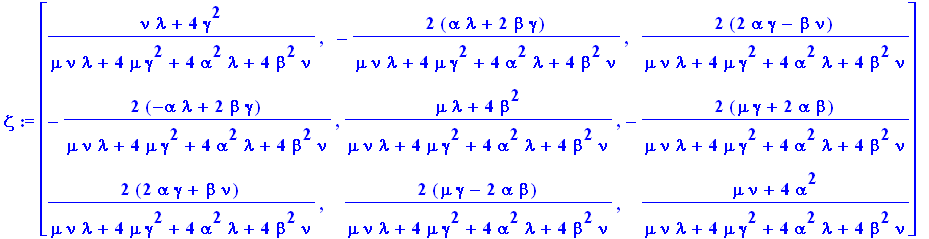
zeta := matrix([[(nu*lambda+4*gamma^2)/(mu*nu*lambda+4*mu*gamma^2+4*alpha^2*lambda+4*beta^2*nu), -2*(alpha*lambda+2*beta*gamma)/(mu*nu*lambda+4*mu*gamma^2+4*alpha^2*lambda+4*beta^2*nu), 2*(2*alpha*gamm...

>   

map(simplify,evalm(S &*  zeta));

matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])

>   

trace(zeta);

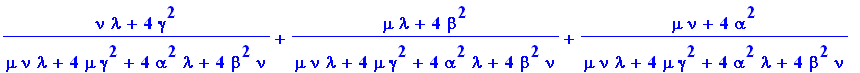
(nu*lambda+4*gamma^2)/(mu*nu*lambda+4*mu*gamma^2+4*alpha^2*lambda+4*beta^2*nu)+(mu*lambda+4*beta^2)/(mu*nu*lambda+4*mu*gamma^2+4*alpha^2*lambda+4*beta^2*nu)+(mu*nu+4*alpha^2)/(mu*nu*lambda+4*mu*gamma^2...

>   

det(zeta);

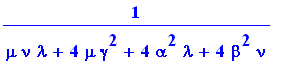
1/(mu*nu*lambda+4*mu*gamma^2+4*alpha^2*lambda+4*beta^2*nu)

>   

normal( trace(zeta) / det(zeta) );

nu*lambda+4*gamma^2+mu*lambda+4*beta^2+mu*nu+4*alpha^2

>   


Cálculo de Autovetores e Autovalores

>   

K:=matrix([[sqrt(2),alpha,beta],[alpha,sqrt(2),alpha],[beta,alpha,sqrt(2)]]);

K := matrix([[2^(1/2), alpha, beta], [alpha, 2^(1/2), alpha], [beta, alpha, 2^(1/2)]])

>   

pc:=charpoly(K, lambda); # Polinômio Característico

pc := lambda^3-3*lambda^2*2^(1/2)+6*lambda-2*alpha^2*lambda-2*2^(1/2)+2*2^(1/2)*alpha^2-2*alpha^2*beta-beta^2*lambda+beta^2*2^(1/2)

>   

factor(%);

(-lambda^2+2*lambda*2^(1/2)+beta*lambda-2-beta*2^(1/2)+2*alpha^2)*(2^(1/2)-beta-lambda)

>   

solve(pc=0,lambda);

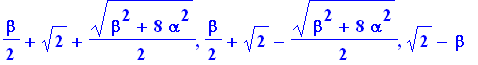
1/2*beta+2^(1/2)+1/2*(beta^2+8*alpha^2)^(1/2), 1/2*beta+2^(1/2)-1/2*(beta^2+8*alpha^2)^(1/2), 2^(1/2)-beta

>   

eigenvals(K);

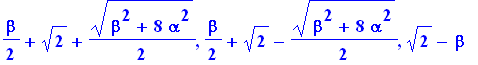
1/2*beta+2^(1/2)+1/2*(beta^2+8*alpha^2)^(1/2), 1/2*beta+2^(1/2)-1/2*(beta^2+8*alpha^2)^(1/2), 2^(1/2)-beta

>   

eigenvects(K);

[1/2*beta+2^(1/2)+1/2*(beta^2+8*alpha^2)^(1/2), 1, {vector([1/2*(1/2*beta+1/2*(beta^2+8*alpha^2)^(1/2))/alpha, 1, 1/2*(1/2*beta+1/2*(beta^2+8*alpha^2)^(1/2))/alpha])}], [1/2*beta+2^(1/2)-1/2*(beta^2+8*...
[1/2*beta+2^(1/2)+1/2*(beta^2+8*alpha^2)^(1/2), 1, {vector([1/2*(1/2*beta+1/2*(beta^2+8*alpha^2)^(1/2))/alpha, 1, 1/2*(1/2*beta+1/2*(beta^2+8*alpha^2)^(1/2))/alpha])}], [1/2*beta+2^(1/2)-1/2*(beta^2+8*...

O resultado é uma lista da forma:

                      [ e_i, m_i,  {  v[1,i],... v[n_i,i] }  ]

onde:

                e_i = são os autovalores
    m_i = multiplicidade
            {v[1,i], ..., v[n_i,i]}  = conjunto de vetores bases

>   

print(K);

matrix([[2^(1/2), alpha, beta], [alpha, 2^(1/2), alpha], [beta, alpha, 2^(1/2)]])

>   


Solução  de B x = v  mediante Gauss-Jordan

>   

B:=matrix(3,3,[19,-50,88,  53,85,-49, 78, 17, 72] );

B := matrix([[19, -50, 88], [53, 85, -49], [78, 17, 72]])

>   

v1:= vector( [3 ,5,-2] ):

>   

v2:= vector( [4 ,-5,9] ):

>   

v3:= vector( [21 ,4,7] ):

>   

augment(B,v1,v2,v3 );

matrix([[19, -50, 88, 3, 4, 21], [53, 85, -49, 5, -5, 4], [78, 17, 72, -2, 9, 7]])

Construímos a matriz aumentada, e invocamos a solução

>   

gaussjord(%);

matrix([[1, 0, 0, 56399/9855, -42938/9855, 43729/3285], [0, 1, 0, -20528/3285, 15761/3285, -15913/1095], [0, 0, 1, -46832/9855, 36584/9855, -35782/3285]])

>   

leastsqrs(B, v1); leastsqrs(B, v2);leastsqrs(B, v3);

vector([56399/9855, -20528/3285, -46832/9855])

vector([-42938/9855, 15761/3285, 36584/9855])

vector([43729/3285, -15913/1095, -35782/3285])

  Funções teste

>   

beta := sqrt(2)*sqrt(5-sqrt(5));

beta := 2^(1/2)*(5-5^(1/2))^(1/2)

>   

A:= matrix([[(sqrt(5)+beta +1)/4, -beta/2 ],[ beta/4 ,( sqrt(5) - beta+1)/4]]);

A := matrix([[1/4*5^(1/2)+1/4*2^(1/2)*(5-5^(1/2))^(1/2)+1/4, -1/2*2^(1/2)*(5-5^(1/2))^(1/2)], [1/4*2^(1/2)*(5-5^(1/2))^(1/2), 1/4*5^(1/2)-1/4*2^(1/2)*(5-5^(1/2))^(1/2)+1/4]])

>   

B:=matrix( [[(sqrt(5)+1)/4,-beta/4 ],[ beta/4,(sqrt(5)+1)/4 ]  ]);

B := matrix([[1/4*5^(1/2)+1/4, -1/4*2^(1/2)*(5-5^(1/2))^(1/2)], [1/4*2^(1/2)*(5-5^(1/2))^(1/2), 1/4*5^(1/2)+1/4]])

 Queremos verificar si A e B são similares, quer dizer,  si existe uma  matriz T, não singular, de maneira que  

   B = T A T^(-1).

>   

issimilar(A,B,'T');

true

>   

map(simplify,T);

matrix([[1, 0], [-1, 2]])

>   


Cálculo Vectorial.

Gradiente

>   

f:= 4*x*y*z - 5*y*x^3;

f := 4*x*y*z-5*y*x^3

>   

gradf:= grad(f,[x,y,z]);

gradf := vector([4*y*z-15*y*x^2, 4*x*z-5*x^3, 4*x*y])

Vetores

>   

v:=vector([4*x-3*x^3*y,7*x*y*z^2+5*y^3,4*x^2*y^2+2*x]);

v := vector([4*x-3*y*x^3, 7*x*y*z^2+5*y^3, 4*x^2*y^2+2*x])

Rotacionais

>   

curlv:= curl(v,[x,y,z] );

curlv := vector([8*y*x^2-14*x*y*z, -2-8*x*y^2, 7*y*z^2+3*x^3])

Jacobianos

>   

jacobian(%,[x,y,z]);

matrix([[16*x*y-14*y*z, 8*x^2-14*x*z, -14*x*y], [-8*y^2, -16*x*y, 0], [9*x^2, 7*z^2, 14*y*z]])

Laplacianos

>   

laplacf:= laplacian(f,[x,y,z] );

laplacf := -30*x*y

Evaluação booleana de expressões

>   

evalb(laplacf = diverge(gradf,[x,y,z]));

true

Diferentes tipos de coordenadas

>   

f := r*sin(theta)*z^2:  v := [r, theta, z]:

>   

gr:=grad(f, v, coords=cylindrical);

gr := vector([sin(theta)*z^2, cos(theta)*z^2, 2*r*sin(theta)*z])

>   

diverge(gr,v, coords=spherical);

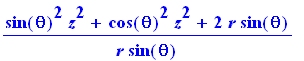
1/r*(sin(theta)^2*z^2+cos(theta)^2*z^2+2*r*sin(theta))/sin(theta)

>   

laph= laplacian(f,v);

laph = -r*sin(theta)*z^2+2*r*sin(theta)

>   

laph= laplacian(f,v,coords=bipolarcylindrical);

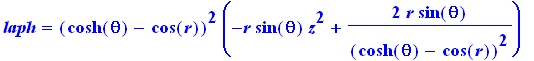
laph = (cosh(theta)-cos(r))^2*(-r*sin(theta)*z^2+2/(cosh(theta)-cos(r))^2*r*sin(theta))

>   

?coords

>   


 

  ====================================================================

 10 Processos em UNIX

nodo5%> maple

        | \ ^ / |              Maple 9  (IBM INTEL LINUX)

._ | \ |        | / | _.     Copyright (c) 2002 by Waterloo Maple Inc.
    \  MAPLE  /          All rights reserved. Maple is a registered trademark of

  <____ ____>        Waterloo Maple Inc.
            |                  Type ? for help.

>  evalf(sqrt(Pi),100);

1.7724538509055160272981674833411451827975494561223871282138077898529112845\
    91032181374950656738544665

> Int( tan(x), x ) = int( tan(x), x );

                             /
                           |
                           |  tan(x) dx = -ln(cos(x))
                           |
                          /


nodo5%> maple < archimap.txt

Com esta instrução   Maple   executará todos os comandos que se encontram não arquivo archimap.txt


nodo5%> maple < archimap.txt > archimap.out


nodo5%> maple < archimap.txt | more


nodo5%> maple -q < archimap > archimap.out

^Z
Suspended
nodo5%> bg
[2] maple -q < archimap > archimap.out &

nodo5%>



============================================

 11 Maple e Latex

Desde que o padrão para incluir gráficos em documentos do Latex usa arquivos poscript, exportaremos os gráficos gerados no ambiente Maple para esse formato. 

  

plot3d((1.3)^x*sin(y), x=-1..2*Pi, y=0..Pi, coords=spherical, style=patch);

criará uma  cornucopia. Para criar o arquivo PostScript para este arquivo, execute o comando

 

 
     plotsetup(postscript, plotoutput=`cornucopia.ps`, 
             plotoptions=`color,portrait,height=300,width=300`);

e  execute o comando plot3d novamente. Em vez de mostrar o gráfico na tela, Maple salva um arquivo Postcript. Abra o arquivo com  ghostview.

Existem duas formas de gerar códigos em Latex. É possível converter uma folha inteira em um arquivo de Latex usando a opção LaTeX e Export As que aparece no menu do File do Maple.

Em lugar de converter um página de trabalho inteira  (worksheet), é possível converter comandos de  Maple  para o  LaTeX diretamente. Maple possui o comando latex que leva expressões matemáticas em linhas de LaTeX. Por exemplo, no ambiente  Maple o comando  latex(sin(x)); volta  como resultado  \sin(x).

 

latex(Int(sin(x),x=0..Pi/4))

\int _{0}^{1/4\,\pi }\!\sin(x){dx}