Next:Divergence
MeasuresUp:Information
and Divergence Measures
Previous:Properties
of Information Measures Go to:Table
of Contents
Distance Measures
Let us consider the following three measures
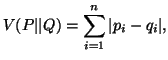
|
|
|
(2.4) |
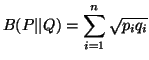
|
|
|
(2.5) |
and
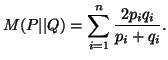
|
|
|
(2.6) |
for all 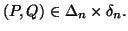
The measures (2.4), (2.5) and (2.6) are famous in the literarture as
the ``Variational distance", the `Bhattacharyya distance"
and the ``Harmonic mean" respectively. These measures satisfy the
following properties
Property 2.15. We have
-
(i)

-
(ii)
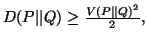
-
(iii)
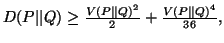
-
(iv)
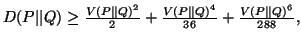
-
(v)
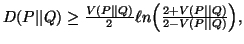
-
(vi)
![$ 2\big[1-B(P\vert\vert Q)\big]\leq V(P\vert\vert Q)\leq \,2\big[2\big(1-B(P\vert\vert Q)\big)\big]^{1/2},$](img549.gif)
-
(vii)
![$ V(P\vert\vert Q)\leq \,2\big(1-B(P\vert\vert Q)^2\big)^{1/2}\leq \,2\big[2\big(1-B(P\vert\vert Q)\big)\big]^{1/2},$](img550.gif)
The measure 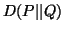 considered here is with natural logarithm base.
considered here is with natural logarithm base.
Property 2.16. We have
-
(i)
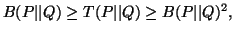
-
(ii)
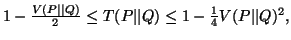
For more details on these measures refer to Mathai and Rathie (1975) [71]
and references therein.
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
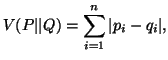
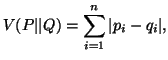
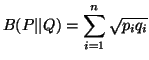
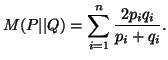
![]()