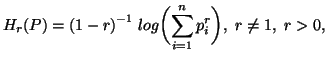 |
(3.1) |
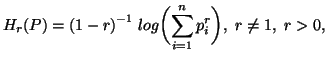 |
(3.1) |
where H(P) is the Shannon's entropy given by (1.7).
Campbell (1965) [20] for the first time,
has shown that the variable lenght version of the elementary coding theorem
carries over to the entropy of order ![]() ,
if one considers exponential lenght and its increasing functions, which
includes, in particular, a generalized lenght in terms of entropy of order
,
if one considers exponential lenght and its increasing functions, which
includes, in particular, a generalized lenght in terms of entropy of order![]() .
Blumer and McEliece (1988) [14] considered
the problem of minimizing redundancy of order
.
Blumer and McEliece (1988) [14] considered
the problem of minimizing redundancy of order ![]() defined in terms of entropy of order
defined in terms of entropy of order ![]() ,
and obtained bounds sharper than that of Gallager (1978) [39].
Taneja (1984a) [101] extended the concept
of exponentiated average codeword lenght of order
,
and obtained bounds sharper than that of Gallager (1978) [39].
Taneja (1984a) [101] extended the concept
of exponentiated average codeword lenght of order ![]() to the best 1:1 codes. For some other aplications of entropy of order
to the best 1:1 codes. For some other aplications of entropy of order ![]() refer to Jelinek (1968a;b) [50] [51],
Jelinek and Schneider (1972) [52], Csiszár
(1974) [29], Nath (1975) [74],
Arimoto (1975; 1976) [4], [5],
Ben-Bassat and Raviv (1978) [11], Kieffer
(1979) [64], Campbell (1985) [22],
Kapur (1983; 1986) [55], [56]
etc..
refer to Jelinek (1968a;b) [50] [51],
Jelinek and Schneider (1972) [52], Csiszár
(1974) [29], Nath (1975) [74],
Arimoto (1975; 1976) [4], [5],
Ben-Bassat and Raviv (1978) [11], Kieffer
(1979) [64], Campbell (1985) [22],
Kapur (1983; 1986) [55], [56]
etc..
Based on the same motivations of Rényi, later researchers (Aczél
and Daróczy, 1963 [1]; Varma, 1966
[119]; Kapur, 1967 [54];
Rathie, 1970 [78], etc..) generalized the
entropy of order ![]() by changing some of its postulates. The generaliation studied by Aczél
and Daróczy (1963) [1], known as entropy
of order
by changing some of its postulates. The generaliation studied by Aczél
and Daróczy (1963) [1], known as entropy
of order![]() is given by
is given by
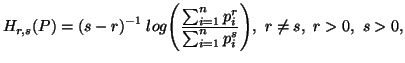 |
(3.2) |
for all ![]() ,
where
,
where ![]() and
and ![]() are real parameters. In particular, when
are real parameters. In particular, when ![]() or
or ![]() ,
the measure (3.2) reduces to (3.1). We can easily verify that
,
the measure (3.2) reduces to (3.1). We can easily verify that
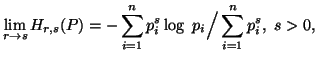
that reduces to Shannon's entropy for![]() .
.