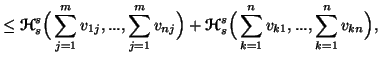A function ![]() will be said structural
will be said structural ![]() entropy
if
entropy
if
In the Rényi's case, Daróczy (1963) [31]
restructured the axioms, while in the Havrda and Charvt's case, Daróczy
(1970) [33] presented an alternative way
to characterize the entropy of degree ![]() .
This is as follows:
.
This is as follows:
Let ![]()
![]() ,
, ![]() be a real valued function satisfying:
be a real valued function satisfying:
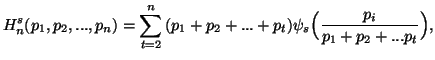
|
|
(3.16) |
and ![]() is as given by (3.3).
is as given by (3.3).
The function ![]() given by (3.16) is famous as
"information function of degree
given by (3.16) is famous as
"information function of degree ![]() ".
".
An alternative way to characterize the entropy of degree ![]() is following the Chaundy and McLeod's (1961) [27]
approach. This can be seen in Sharma and Taneja (1975) [92],
and is as follows:
is following the Chaundy and McLeod's (1961) [27]
approach. This can be seen in Sharma and Taneja (1975) [92],
and is as follows:
Let ![]()
![]() be a real valued function satisfying
be a real valued function satisfying
![]()
for all ![]() ,
and
,
and
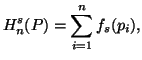
Some alternative approaches to characterize the measure (3.51) can be seen in Aczél and Daróczy (1975) [2], Mathai and Rathie (1975) [71] and Taneja (1979) [99].
It is worth emphasizing here that the measure (3.3), or better ![]() ,
, ![]() satisfies some extra properties given below.
satisfies some extra properties given below.
Property 3.18. We can write
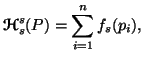

Property 3.20. Let ![]() ,
then
,
then
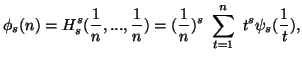
Property 3.22. For all ![]() ,
, ![]() ,
,![]() ,
we have
,
we have
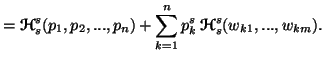
![]()