Next:Noiseless
Coding and GeneralizedUp:Entropy
of Degree and
Previous:Mutual
Information of Degree Go to:Table
of Contents
Properties of Conditional Entropies
of Degree s
We have the following properties:
Property 6.17. For all 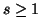 ,
we have
,
we have
-
(i)
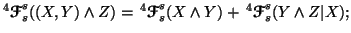
-
(ii)
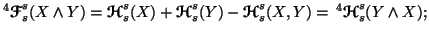
-
(iii)
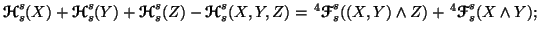
-
(iv)
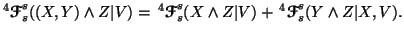
Property 6.18. For all 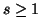 ,
we have
,
we have
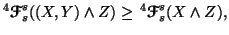 with equality iff
with equality iff  and
and  are independent given
are independent given  .
.
Property 6.19. For all 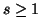 ,
we have
,
we have
-
(i)
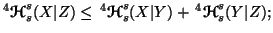
-
(ii)
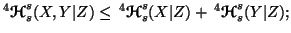
-
(iii) If
 ,
then
,
then
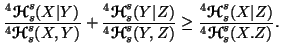
Property 6.20. Let

 and
and
 then, we have
then, we have
-
(i)
 and
and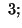
-
(ii)
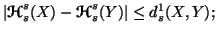
-
(iii)
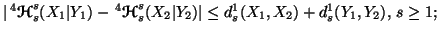
-
(iv)
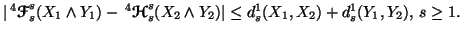
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
![]() ,
we have
,
we have
![]() ,
we have
,
we have