graddescendente.html

Metodo do gradiente descendente

Worksheet by Aldrovando Luis Azeredo.
MTM 5170 Calculo 3A

2000/1

Introducao:

Para limpar a memoria do Maple e nao carregar nenhum lixo para seu programa vamos comecar fazendo uma lobotomia no Maple. Execute:

> restart:

> Digits:=20:

Exposicao do Metodo:

Um dos metodos que vimos em aula para encontrar um minimo local baseia-se na propriedade do gradiente indicar a direcao de maximo crescimento da funcao. Este metodo se chama Metodo do Gradiente Descendente . Considerando sua complexidade numerica so podemos implementa-lo com auxilio dos computadores. Vamos utilizar o Maple para exemplifica-lo:

Comecamos definindo a funcao.

> func := (x,y) -> (x-2)^2+(y-3)^2+sin(x)*cos(y);

Observe que esta funcao eh uma mistura de polinomio e funcoes trigonometricas e sera muito dificil obter a solucao da equacao . Assim podemos utilizar nosso metodo para obter uma aproximacao razoavel deste minimo.

Como o Maple pode fazer graficos 3D sera util plotarmos a funcao e ver o que esta acontecendo. Como primeira aproximacao para o minimo local escolhemos o ponto (2, 3). Vamos plotar esta funcao na vizinhanca deste ponto, por exemplo de raio 1.

> a := 2: b := 3: del := 1: evalf(func(a, b));
plot3d(func(x,y),x=a-del..a+del, y=b-del..b+del,
axes=boxed, style=patchcontour);
plots[contourplot](func(x,y),x=a-del..a+del, y=b-del..b+del);

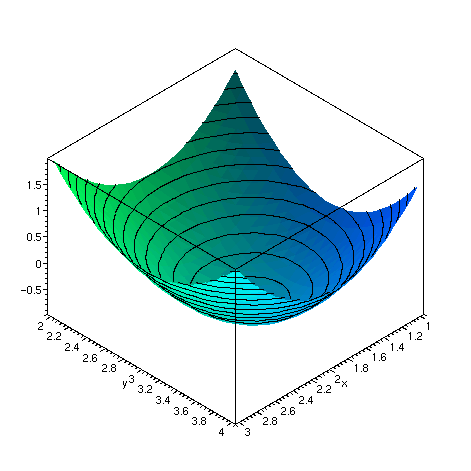
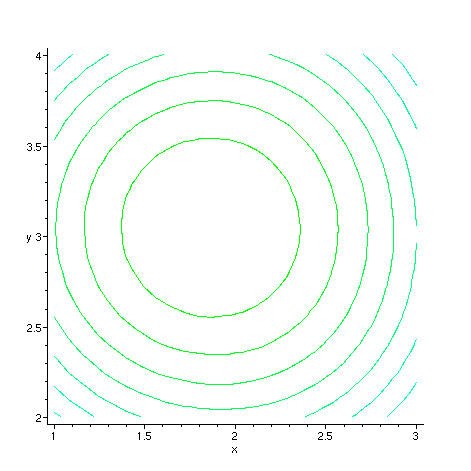
Esta claro que estamos proximos do minimo. Vamos usar nosso metodo para obte-lo. Observe que nosso metodo depende da escolha da primeira aproximacao.

A estrategia do metodo consiste em tomarmos a direcao de maior decrescimento, a saber a direcao oposta do gradinte e nos movermos um pouco. Para tal precisamos calcular o gradiente de f.

> funcx := diff(func(x,y),x);
funcy := diff(func(x,y),y);

Agora calculamos as derivadas parciais no ponto inicial.

> fxpoint := evalf(subs({x=a, y=b}, funcx));
fypoint := evalf(subs({x=a, y=b}, funcy));

O metodo consiste em iterar a expressao

com o cuidado de escolher pequeno suficiente para que

e nao tao pequeno para que o processo de aproximacao nao se torne lento demais. (Vamos pois olhar para f restrita a curva parametrizada

[a+fxpoint*t, b+fypoint*t].) Como estamos querendo o ponto de minimo nesta secao, tomamos a derivada desta funcao e igualamos a zero.

> plot(func(a+fxpoint*t, b+fypoint*t), t=-1..0);

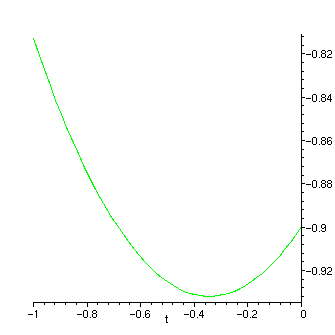
A sintaxe do comando fsolve pode ser obtida clicando-se com o mouse sobre o link fsolve

> pathdiff := diff(func(a+fxpoint*t, b+fypoint*t),t);
tmin := fsolve(pathdiff,t);

Segue que a nova aproximacao sera. Observe que o valor de f decresceu comparativamente ao valor no ponto inicial.

> a1 := a + tmin*fxpoint; b1 := b + tmin*fypoint; func(a1, b1);

Agora vamos tornar esta processo iterativo automatico. Para tal construiremos uma procedure que se encarregara de fazer o numero de iteracoes que pedirmos.

Procedure: ajusta

A seguinte procedure ajusta calcula a aproximacao pedida dado a posicao inicial e o numero de iteradas requeridas pelo usuario. O numero de iteracoes sera introduzido pelo usuario no decorrer do processo. O comando readstat espera que apos digitado o numero voce devera digitar " ; " .

> ajusta:=proc(x0,y0::numeric)

> local a1,b1, i,a,b,tmin,fxpoint, fypoint, pathdiff: global af, bf, valordaf,n: a1:=x0: b1:=y0:

> n:=readstat("Entre com o numero de iteracoes: apos digitar termine com ; ");

> while not type(n, integer) do ERROR("A positive integer is expected "); n := readstat("Por favor, entre novamente com o numero de iteracoes"); od;

> for i from 1 to n do
a := a1; b := b1;
fxpoint := evalf(subs({x=a, y=b}, funcx));
fypoint := evalf(subs({x=a, y=b}, funcy));
pathdiff := diff(func(a+fxpoint*t, b+fypoint*t),t):
tmin := fsolve(pathdiff,t);
a1 := a + tmin*fxpoint; b1 := b + tmin*fypoint; func(a1, b1);
od:

> valordaf:=func(a1, b1);

> print("Valor de x final "=a1, "Valor de y final "=b1, "Valor da f no ponto encontrado "= valordaf);

> print(`gradiente final `=[fxpoint,fypoint]);

>

> end:

> ajusta(20,43);

Entre com o numero de iteracoes: apos digitar termine com ; 10;

Programa passo a passo:

> func := (x,y) -> (x-2)^2+(y-3)^2+sin(x)*cos(y);
initx := 20; inity := 43;
funcx := diff(func(x,y),x);
funcy := diff(func(x,y),y);
a1 := initx: b1 := inity:
for i from 1 to 10 do
a := a1; b := b1; valordaf := evalf(func(a, b));
print(`valor atual de a `=a, `valor atual de b `=b, ` valor da f `= valordaf);
fxpoint := evalf(subs({x=a, y=b}, funcx));
fypoint := evalf(subs({x=a, y=b}, funcy));
print(` gradient `=[fxpoint,fypoint]);
pathdiff := diff(func(a+fxpoint*t, b+fypoint*t),t);
tmin := fsolve(pathdiff,t);
a1 := a + tmin*fxpoint; b1 := b + tmin*fypoint; func(a1, b1);
od: