> with(plots):

Newton's Method

We want to solve the equation where using Newton's method . This method is described in the text, and you may want to review the discussion there. Recall how the method works. First, we make an initial guess and then make sucessive approximations to a solution by using the formula

where denotes the derivative of .

To begin our example, specify the function with the Maple command:

> f:= x -> x^3 -8*x - 5;

Next plot it to get an idea where the root(s) are. We pick a range somewhat arbitrarily and hope that at least one root is in that range. Since is a cubic equation, we would generally expect three roots, but some of them might be non-real complex numbers.

> plot(f(x), x=-5..5,y=-20..20);

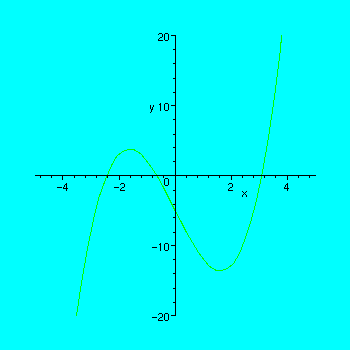
In this particular case, there appear to be three real roots located at about 3, -1, and -2.5.

>

To use Newton's method we need the derivative, which we determine by applying Maple's D operator to the function . Note that we need to put parentheses around the function name. To save writing and simplify the notation, we shall call the derivative function .

> g := D(f);

You should note that the expression on the right is in fact the derivative of the original expression defining .

In order to get sufficient accuracy we specify that Maple should calculate and display 20 significant digits.

> Digits:= 20;

Let's first see if we can find the root near to a reasonable degree of precision. We start with 3.0 as the initial guess.

> x[0]:= 3.0;

Now we apply the Newton's Rule formula to get 5 successive approximations.

> x[1]:=x[0] - f(x[0])/g(x[0]);

> x[2]:= x[1] - f(x[1])/g(x[1]);

> x[3]:= x[2] - f(x[2])/g(x[2]);

> x[4]:= x[3] - f(x[3])/g(x[3]);

> x[5]:= x[4] - f(x[4])/g(x[4]);

Since is the same as to 20 signifcant places places, there does not seem much point in computing further approximations. We certainly seem to have calculuated the desired root to that many signifcant places, so we stop.

>

Now let's do the same thing again without using the intricate subscript or index notation. This is a bit subtle so make sure you understand it.

Call the `current approximation ` '. According to the Newton's Method rule, the next approximation is

(Recall is our shorthand for the derivative of .) However, the Maple assigment statement

a := a - f(a)/g(a),

has exactly the effect of replacing the old value of by the new value obtained by the Newton's Method formula. So start off with the same guess for a starting approximation.

> a:= -2.5;

Now just repeat the following statement at least five times (or more if you want), and observe what happens to the value of . (To repeat the statement, simply use the mouse to reposition the cursor on the first line of the pair of statements below.) The purpose of the first line is to exhibit the last value of before changing it so you can compare successive values

> a:=a;
a := a - f(a)/g(a);

Homework

Warning: In the problems which follow, you may find as you repeat the procedure that the value of does not start repeating but rather the last digit oscillates between two values. This is an artifact of rounding. Were we able to do infinite precision arithmetic, this phenomenon would not occur. However, since we don't have that option, we may have to be satisfied with only 19 significant digits. (Or, we could increase the number of significant digits by using the `Digits := ...' command and push the oscillation further out.)

Problem 1. (a) Find the root near -1.0 by changing the initial guess to -1.0 two commands above and then iterating the above line until you get a stable answer. Keep count of the number of times you had to do the iteration. Write it down or enter the answers as text below.

The second root to 19 or 20 significant figures is

The number of iterations required was

(b) Do the same for the root near -2.5.

The third root to 19 or 20 significant digits is

The number of iterations required was

Problem 2. Try the initial guess

> a := 1.3;

This is actually closest to the root near x = 3.0, so you might expect the iterations to converge to the root nearest that value. Repeatedly execute the code below (by repostioning the cursor as before), and you will see both the successive values of the most current approximation and the plots showing how the tangent line, whose intersection with the x-axis gives you the next approximation, moves around. Then write a short paragraph explaining what happened.

> plot({f(x),f(a)+g(a)*(x-a)},x=-6..6,y=-20..20);

> a:=a;a:= a - f(a)/g(a);

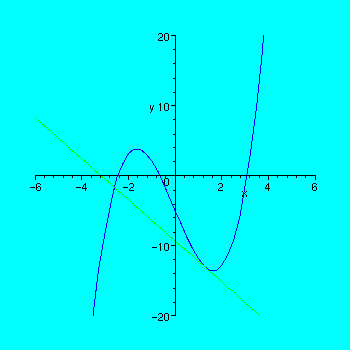
Problem 2. Use Newton's method to find a root of the equation in the interval [-4,4] by executing the code below. But notice that you will have to choose an initial guess in the interval by replacing `????' by an appropriate number. Circle what you think the answer is to the degree of accuracy obtainable with Maple's current settings. How many iterations were required?

> f := x -> x - 3*cos(x);
g := D(f);

> plot(f(x),x=-4..4);

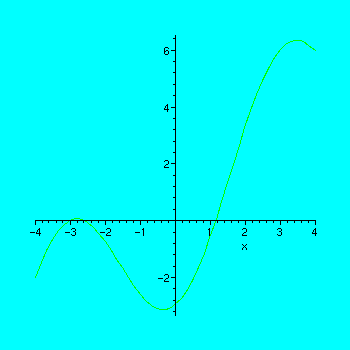
> a := 2; a := 1.0*a;

> a:=a; a:= a - f(a)/g(a);

Note for the curious . '1.0*a' should be the same as 'a', but expressing it that way tells Maple it should be dealing with a floating point number rather than a rational number. Maple will try to avoid evaluating cos(a) and sin(a) if it thinks a is rational since it can't give an exact answer, which would complicate the situation. If you are curious, take out the 'a = 1.0*a' above and execute the code over again to see what happens.