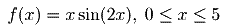

Para encontrar o máximo e o mínimo absolutos da função
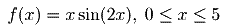
nós calculamos a derivada
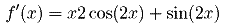
e procuramos os zeros da derivada que são:
Estes são os únicos pontos críticos de f. Considere a seguinte tabela dos valores da f nos pontos críticos e nos pontos extremos do intervalo [0,5]:
| x | f(x) |
|---|---|
| 0 | 0 |
| 5 | -2.72010... |
| 1.01437... | 0.90985... |
| 2.45658... | -2.40723... |
| 3.90933... | 3.95836... |
de onde podemos ver que o máximo absoluto ocorre em x = 3.90933... e é 3.95836... e o mínimo absoluto ocorre em x = 5 e é -2.72010....