Funções gráficos propriedades e aplicações:

Colocação do problema: Utilidade das funções.

Informação do Censo dos USA:

O seguinte conjunto de dados é fornecido pelo censo americano:

> pop:=[3.929214, 5.308483, 7.239881, 9.638453, 12.866020, 17.069453,
23.191876, 31.433321, 39.818449, 50.155783, 62.947714,
75.994575, 91.972266, 105.710620, 122.775046, 131.669275,
151.325798, 179.323175, 203.302031, 226.545805, 248.709873];

Podemos organizar estes dados como uma coleção de pontos com o tempo no eixo horizontal e a população no eixo vertical, observando que o primeiro dado se refere ao ano de 1790 e que o intervalo de cada censo é de 10 anos.

> tt:=[seq(i*10,i=0..20)]:
Poppts:=[seq([tt[i]+1790,pop[i]],i=1..21)];

E agora nós fazemos um gráfico destes pontos:

> plot(Poppts,style=POINT);

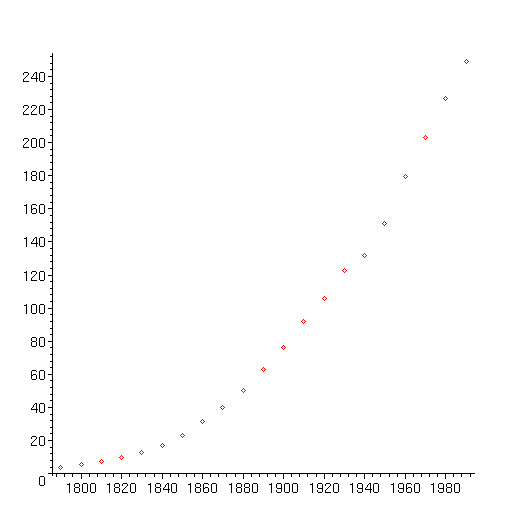
Problema1

Como podemos aproximar este conjunto de dados por uma função suave?.

Uma função suave ajustando os dados:

A seguinte função fornece um ajuste suave para os dados acima. Ela e conhecida como o ajuste Logistico para os dados populacionais.

> P:=t->387.9580209/(1+54.08120241*exp(-0.02270347336*(t-1790)));

Para vermos quão boa é tal aproximação nós desenhamos simultaneamente os dois gráficos.

> J:=plot(Poppts,style=POINT):
K:=plot(P(t),t=1790..1990):

> plots[display]({J,K});

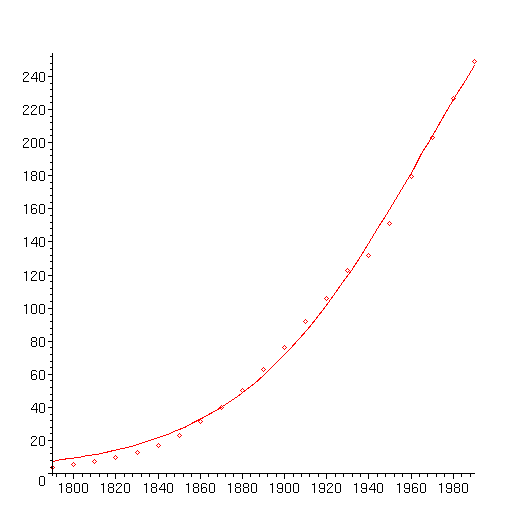
Problema 2

Em que ano a população americana estava crescendo mais rapidamente?

Ano de crescimento mais rapido da população:

Usamos a aproximação obtida e procuramos o máximo da derivada desta função. Para tal encontramos o ponto onde a segunda derivada é zero.

> T:=solve((D@@2)(P)(t)=0,t);

A resposta sugere o ano correto, no entanto o ano não pode ser fracionário e teremos que interpretar.

Funções:

Definição:

Exemplos:

Exemplo1. A regra que associa a idade de cada aluno na sala é uma função.

Exemplo 2. A seguinte equação matemática  determina uma função.

> f:=x->2*x-1:

> plot(f(x),x=0..10);

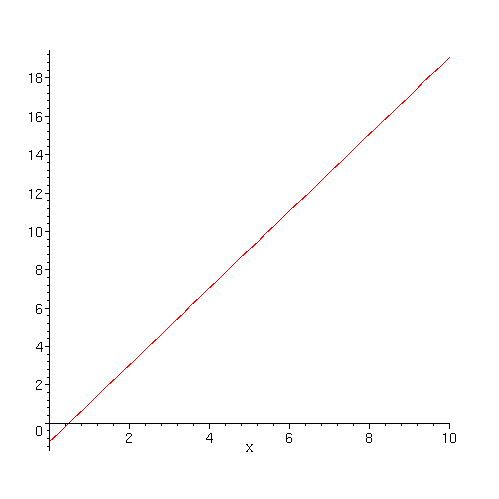
Definição: Uma função de uma conjunto A em conjunto B é uma regra que associa a cada elemento do conjunto A um unico elemento do conjunto B. A denomina-se domínio da função.

Usualmente denotamos uma função pela letra  e escrevemos  para denotar o valor que a função associa ao ponto  .

Exemplos:

As funções que normalmente trabalharemos são funções numéricas, isto é aquelas para as quais os conjuntos A e B da definição são subconjuntos dos números reais  . E são definidas por expressoes matemáticas como as abaixo ainda que não seja o modo preciso de se referir a uma função pois não há na definição a especificação dos conjuntos A e B. A se denomina domínio de f e B contradomínio de f .

> f1:=x->x^3-6*x+6;

> f2:=x->sqrt(x-2);

> f3:=t->1/(t^2-t-2);

> f4:=x->x^2-4*x+1;

Exercício 1:

Encontre os domínios das funções definidas acima.

Exercício 2:

Os custos de uma indústria de bens usualmente consiste de dois tipos. Os custos fixos e os custos variáveis. Se uma fábrica de bicicletas tem custo fixo de $500 por semana e custo variável de $30 por bicicleta, encontre uma equação para o custo total na produção de  bicicletas por semana.

Exercício 3:

Suponhamos que a fábrica do exemplo anterior venda suas bicicletas por $80 cada.Encontre a função ganho associada com a variavel  .

Exercício 4:

A fábrica de bicicletas quer ter lucro naturalmente. Encontre a função lucro como função de  . Determine os valores  para os quais  é positiva.

Gráfico de funções:

O gráfico de uma função é o desenho no plano cartesiano XY dos pontos do domínio e seus correspondentes valores associados pela função dada. Normalmente especificamos uma parte do domínio da função dada quando queremos desenhar o gráfico.

Exemplos: Vamos plotar os gráficos das funções que selecionamos mais acima.

Exemplo 1:

Exemplo 2:

> plot(f2(x),x=2..20):

Exemplo 3:

> L:={solve(t^2-t-2=0)};

> plot(f3(x),x=2..10);

>

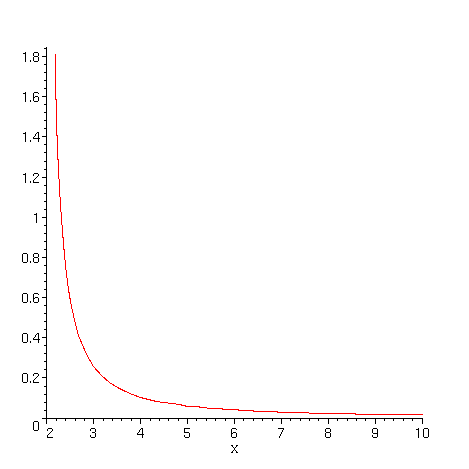
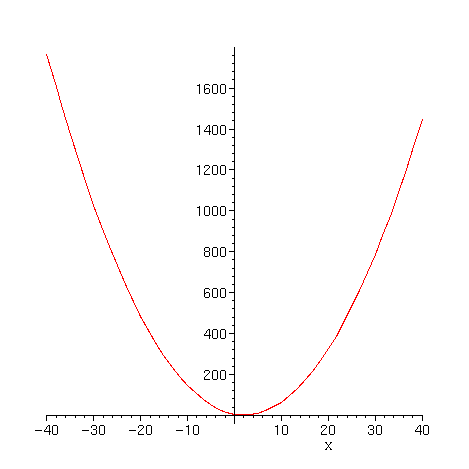
Exemplo 4:

> plot(f4(x),x=-40..40);

>

Exemplo 5:

> f5:=x->abs(x^3-4*x-3):

> plot(f5(x), x=-2..2):

Tipos de funções usuais:

Potências:  onde n denota um número natural.

> with(plots):

> p1:=plot(x^2,x=-1..1,color=blue):

> p2:=plot(x^3,x=-1..1,color=gold):p3:=plot(x^3,x=-1..1,color=red):

> p4:=plot(x^4,x=-1..1,color=black):p5:=plot(x^5,x=-1..1,color=brown):

> display({p1,p2,p3,p4,p5},title=`Potências`):

Funções Racionais:  onde P(x) e Q(x) são polinomios.

> r:=x-> x/(x-2):

> plot(r(x),x=1..3,y=-10..10):

Potências generalizadas :  onde r denota um número racional.

Definições fundamentais:

a)  sinificando x . x . x . . . x (n fatores):

b)  significando  sempre que x é diferente de zero.

c)  significando  com  se n é par.

d)  significando  .

e)  significando 1 sempre que x é diferente de zero.

Exemplo :

> plot(x^(1/3),x=1..100):

> plot(x^(-3/2),x=1..10):

Teorema:( Lei dos expoentes).

Zeros de funções:

É um problema bastante usual a determinação dos intervalos onde uma dada função é positiva ou negativa isto é onde  tem o mesmo sinal. Para tal precisamos saber os pontos onde as funções assumem o valor zero. Para o nosso interesse agora usaremos o seguinte princípio:se a expressão de  puder ser fatorada em vários produtos então os zeros de  são os zeros dos fatores separadamente.

Exemplo1:

Encontre os zeros de  .

Observe que podemos escrever  . Logo os zeros de cada fator sao  e  . Segue pelo argumento acima que os zeros de  sao  . Veja pelo gráfico que nosso resultado está correto.

> plot(x^2-3*x-4,x=-2..5):

Exercício 1:

Exercício 2:

Um fábricante de ar condicionado sabe que o custo total em produzir x unidades por semana e de  reais. Se o fábricante pode vender cada unidade por  reais, quais são os valores de produção que correspondem a ter lucro.

Exercício 3:

Aplicação a economia : Funções demanda e oferta .

Sob certas condições de mercado o preco de venda de um produto determina o número de itens que os consumidores irão comprar em certa unidade de tempo. Se denotamos por  o número de itens que serão vendidos ao preco  durante o intervalo de tempo
Então  se chama a função demanda. A propriedade fundamental que regula esta função e que precos altos correspondem a procura baixa., chamada lei da demanda.

Similarmente, a função que associa o número de itens que os consumidores vao comprar com preco  por unidade de tempo se chama função oferta e denotamos por  . De modo geral, precos de venda altos correspondem a altos níveis de oferta. A figura abaixo ilustra os gráficos de  e  .

> p1:=plot( p^3, p=0.5..2,color=red):

> p2:=plot(1/p^3,p=0.5..2,color=blue):

> with(plots):

> display({p1,p2});

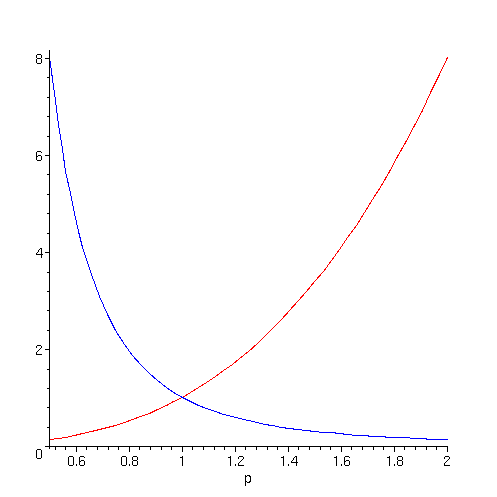
O ponto de interseção dos dois gráficos denomina-se ponto de equilíbrio. Ele indica o preco ideal no qual todo aquele interessado em comprar o produto poderia comprá-lo e não haveria oferta em excesso . O objetivo do mercado é determinar tal ponto.

Exercício:

Combinando funções: operações e composição:

Combinando algebricamente:

Podemos combinar funções conhecidas e obter novas funções usando as operações algébricas.

Definição: Dadas  ,  e um número  , as funções  ,  ,  ,  e  sao definidas

pelas seguintes expressoes:

a) 

b) 

c) 

e)  

f)  sempre que  é diferente de zero.

Exemplo:

Sejam  e  . Então

a) Se  calcule  e  . Como

tem-se  e  .

b) Se  calcule  . Como

temos que  .

Composição de funções:

Definição:

Dadas duas funções  e  a função composta  é a função resultado da ação da função  agindo nos valores da função  . Isto e,

Exemplo 2:

Se  e  determine  .

isto e  e portanto  .

Exercício 1 :

Sejam as funções  ,  e  . Determine

a) 

b) 

Exercício 2:

Se  encontre  tal que  .

Exercício 3:

Faca o gráfico da função  definida por:  se  e  se  .