Cálculo C
Lista I
Exercício 1
Um peso de
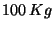
está colocado como na figura 1.
Determine as tensões
T1,
T2 em ambos os fios.
Exercício 2
Faça o mesmo que na primeira questão para a figura seguinte:
Exercício 3
Considere uma força
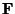
atuando sobre um corpo rígido
sobre um ponto
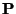
dada por um vetor
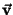
como na figura 3.
O
torque (relativo a origem ) define-se como
Encontre o torque em P se uma força de 13 Kg está aplicada
como nafigura abaixo:
Exercício 4
Encontre as equações dos planos determinados por:
- 1.
- três pontos,

- 2.
- pelo ponto (6, 5,-2) e paralelo a x+y-z=1.
- 3.
- pelo ponto (1,4,5) e com normal
 .
.
- 4.
- pela reta interseção dos planos
x-z=1, e y+2z=3 e é perpendicular ao plano x+y-2z=1.
Exercício 5
Encontre as equações paramétricas dos planos
do exercício anterior.
Exercício 7
Encontre os limites:
- 1.
-
- 2.
-
- 3.
-
Exercício 8
Encontre as equações paramétricas das retas tangentes as curvas abaixo nos pontos dados:
- 1.
-

- 2.
-
 .
.
- 3.
-
 .
.
Exercício 9
As curvas
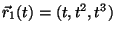
e
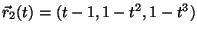
se interceptam na origem. Encontre o ângulo de interseção neste ponto.
Exercício 10
Considere a curva que é a interseção do cilindro x2+y2=4e do cilindro z=x2. Encontre uma parametrização para esta curva.
Exercício 12
Um projetil é lançado da origem como na figura 5.
- 1.
- Encontre a posição do projétil em função do tempo
- 2.
- Determine o ângulo de elevaçào
 que maximizará a distância
sobre o plano inclinado.
que maximizará a distância
sobre o plano inclinado.
Exercício 13
Uma bola rola sobre uma mesa com velocidade
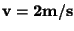
.
Esta mesa tem
3.5 m de altura.
- 1.
- Determine o ângulo
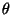 com o qual a bola bate no solo
e também a velocidade vertical no ponto de impacto.
com o qual a bola bate no solo
e também a velocidade vertical no ponto de impacto.
- 2.
- Suponha que a bola rebate do solo com o mesmo ângulo, mas ,
devido a perda no impacto perde
 de sua velocidade ali.
Determine o ponto do próximo impacto com o solo.
de sua velocidade ali.
Determine o ponto do próximo impacto com o solo.
Exercício 14
Uma partícula se move com velocidade angular constante
w ao longo de um círculo cujo centro
está sobre a origem e de raio R. Suponha que o movimento é anti-horário e que a partícula está no ponto (R,0)quando t=0. A posição em função de t se escreve
- 1.
- Encontre a velocidade
 e mostre que
e mostre que
Conclua que  é tangente ao círculo e aponta na direção do movimento.
é tangente ao círculo e aponta na direção do movimento.
- 2.
- Mostre que a velocidade
 da partícula é a
constante
da partícula é a
constante  .
O período T da partícula é o tempo
de uma revolução completa. Conclua que
.
O período T da partícula é o tempo
de uma revolução completa. Conclua que
- 3.
- Encontre o vetor aceleração
 .
Mostre que é proporcional a
.
Mostre que é proporcional a  e que aponta para a origem. Uma aceleração com esta propriedade
é chamada aceleração centrípeta. Mostre que
e que aponta para a origem. Uma aceleração com esta propriedade
é chamada aceleração centrípeta. Mostre que
- 4.
- Suponha que a partícula tenha massa m. Mostre que a magnitude da força
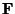 requerida para produzir este movimento, chamada força centrípeta
é
requerida para produzir este movimento, chamada força centrípeta
é
Exercício 15
Seja a curva parametrizada
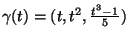
,
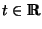
representando o movimento de um
corpo. Suponha que no instante
t=1 o corpo se desprende da curva
e continua seu movimento sem forças atuando sobre ele. Determine o ponto e o
instante
no qual o corpo encontra o plano x+y+z=10
Exercício 16
Encontre o ângulo entre os planos x+y+z=1 e
x-2y+3z=1.
Exercício 17
Encontre uma fórmula para a distância de um ponto
P1=(x1,y1,z1)e o plano
ax+by+cz=d.
Exercício 18
Encontre as equações paramétricas da curva interseção
dos planos x+y-z=2 e
3x-4y+5z=6.
Exercício 19
Encontre as equações paramétricas das retas tangentes
as curvas abaixo nos pontos considerados:
- 1.
-
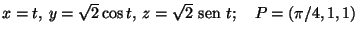
- 2.
-
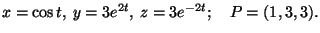
Exercício 20
Uma partícula se move de acordo com a lei
Encontre as componentes normal
e tangencial da aceleração.
Exercício 21
Uma curva circular de raio
R em uma auto-estrada é inclinada
com ângulo de inclinação
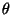
de modo que um carro
pode rodar por ela sem derrapagem quando nao há atrito nenhum
entre o carro e a estrada. A velocidade máxima na qual um
carro pode
atingir sem derrapagem denota-se  .
Suponha que um carro de massa m a está atravessando
com velocidade
.
Suponha que um carro de massa m a está atravessando
com velocidade  .
Duas forças agem sobre o carro:
a força verticall, mg devido ao peso do carro e uma força
.
Duas forças agem sobre o carro:
a força verticall, mg devido ao peso do carro e uma força 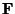 exercida pela estrada e normal a ela.
exercida pela estrada e normal a ela.
(Veja figura)
A componente vertical de 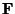 equilibra o peso do carro, logo
equilibra o peso do carro, logo
A componente horizontal de
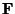
produz a força centrípeta
sobre o carro e portanto de acordo com a segunda lei de Newton e da
parte (d) do exercício anterior
é:
- 1.
- Mostre que
- 2.
- Encontre
 para uma curva circular de raio 400 m cujo
ângulo de inclinação
é 120.
para uma curva circular de raio 400 m cujo
ângulo de inclinação
é 120.
- 3.
- Suponha que os engenheiros querem manter o ângulo mas
desejam aumentar
 em
em  .
Qual deveria ser o raio da curva?
.
Qual deveria ser o raio da curva?
Exercício 22
Uma estrada tem a configuração da parábola
120 y=x2.
Um caminhão está carregado de tal modo que irá tombar se a componente
normal de sua aceleração exceder 30. Que valores de
velocidade
garantirão uma passagem sem desastre pelo vértice da parábola?
Aldrovando Azeredo Araujo
1999-05-21
![\includegraphics[width=0.60\textwidth]{fig3.eps}](img9.gif)
![]() .
Suponha que um carro de massa m a está atravessando
com velocidade
.
Suponha que um carro de massa m a está atravessando
com velocidade ![]() .
Duas forças agem sobre o carro:
a força verticall, mg devido ao peso do carro e uma força
.
Duas forças agem sobre o carro:
a força verticall, mg devido ao peso do carro e uma força ![]() exercida pela estrada e normal a ela.
exercida pela estrada e normal a ela.
![]() equilibra o peso do carro, logo
equilibra o peso do carro, logo