Lista II
Cálculo C
Nos próximos exercícios daremos algumas aplicações dos
resultados obtidos sobre curvas, entre elas
obteremos algumas parametrizações de curvas clássicas.
Exemplo 1 (A Catenária.)
O problema consiste em obter a curva que
representa
um fio inextensível de densidade de massa uniforme, suspenso
sob ação apenas da gravidade como
na figura 1
Suponhamos a parametrização natural:
Seja
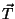
a tensão em um ponto genérico e
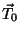
e tensão no
ponto mais baixo
atingido pelo fio. Associemos a esse ponto o parâmetro
t0.
Então como mostra a figura o equilíbrio de forças implica as
equações:
onde
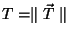
e
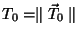
.
Agora usamos a fórmula do comprimento para obtermos a expressão do peso
do pedaço de fio considerado de
t0 até
t.
Dividindo uma equação pela outra obtemos
Usando que
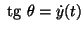
,
podemos escrever
Derivando esta expressão em relação a t obtemos:
Mais adiante saberemos como encontrar uma expressão para y(t). Por
enquanto por
verificação o aluno pode
se certificar que
serve e portanto que
Exercício 1
Determine a curva descrita por um fio de comprimento 120m, suspenso entre
dois postes
distando 100m e tal que a altura de um poste seja 90m e a do outro 100.
Exemplo 2 (A Tractriz)
Neste exemplo consideramos um objeto colocado sobre o
ponto
do plano (
a,0) e que está sendo puxado na direção do eixo
y
positivo como na figura.
através de uma corrente de comprimento
a.
Figure 2:
Tractrix clássica
|
|
Da figura 2 obtem-se facilmente que se a curva está parametrizada
via
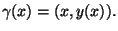 então
então
e usando trigonometria temos que
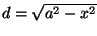
e finalmente
Por integração encontramos a expressão de
y e portanto de
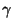
:
Exercício 2
Modele o mesmo problema com as seguintes condições : o objeto
se encontra no ponto (0,a) e está sendo puxado na direção do eixo
X positivo
Exercício 3
Considere uma criança andando no plano e arrastando seu brinquedo
que está conectado à criança por uma barra rígida de
comprimento
a.
Seja
(
x(
t),
y(
t)) a posição do
brinquedo em cada instante de tempo. Determine as equações que regem
este
problema. Seja
(
X(
t),
Y(
t)) a posição do menino. O seguinte desenho
pode ajudá-lo muito.
Figure 3:
A criança e o brinquedo
|
|
Exercício 4
Neste exercício voce deverá modelar o seguinte problema: considere um
corredor seguindo sua trajetória que a partir de determinado momento
passa a ser perseguido por um cão que suporemos ter velocidade escalar
constante. Seja
(
X(
t),
Y(
t)) a trajetória do corredor que é um dado de
seu problema, e seja
(
x(
t),
y(
t)) a tragetória do cão que estava
em (
x0,
y0) no instante
t=0 quando começou a perseguição.
Seja
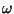
o módulo da velocidade do cão. A hipótese fundamental é que a velocidade do cão está
sempre apontando para o corredor. Modele esta situação.
Exercício 5
Encontre uma parametrização para a astróide cuja equação cartesiana
é:
x2/3+y2/3=a2/3
Exercício 6
A curva de Agnesi é uma curva em forma de sino que é definida como
se segue: considere um círculo de raio
a e centro em (0,
a) como na
figura.
Figure 4:
Curva de Agnesi
|
|
Para cada
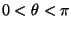 considere a reta com inclinação
considere a reta com inclinação
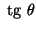 passando pela origem. Esta reta intercepta o círculo no ponto B e também
intercpta a reta y=2a em um ponto A. O ponto da curva de agnesi
correspondente tem como coordenadas x a coordenada x de A e y a
coordenada y de B. Determine uma parametrização para a curva de Agnesi
usnado como parâmetro o ângulo
passando pela origem. Esta reta intercepta o círculo no ponto B e também
intercpta a reta y=2a em um ponto A. O ponto da curva de agnesi
correspondente tem como coordenadas x a coordenada x de A e y a
coordenada y de B. Determine uma parametrização para a curva de Agnesi
usnado como parâmetro o ângulo 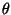 .
.
Solução:
Exercício 7
Uma partícula se move em um disco em direção à fornteira, e sua posição
é dada por
onde
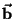
é um vetor unitário, que está rodando juntamente com o disco
com velocidade angular constante
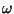
no sentido anti-horário (Fig 5). Encontre
aceleração
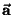
da partícula.
Figure 5:
Aceleração de Coriolis
|
|
Solução: Pela rotação podemos escrever
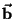 da forma,
da forma,
Derivando obtemos a velocidade
Obviamente
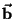
é a velocidade da partícula relativamente
ao disco, e
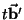
é a velocidade adicional devida à rotação.
Derivando mais uma vez, obtemos a aceleração:
É fácil ver que
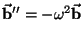
e portanto
este último termo na equação acima aponta para o centro do disco e portanto é a aceleração
centípeta devida à rotação. O termo mais interessante é
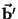
,
chamado de aceleração de Coriolis que resulta da interação da rotação do disco com o movimento da partícula Ele tem a direção de
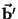
isto é é tangencial à fronteira do disco e em referência
ao sistema fixo XY aponta na direção da rotação.
Exercício 8
Encontre a aceleração de um projétil
P se movendo ao longo
de um meridiano M de uma esfera em rotação com velocidade constante relativa à esfera, que rota com velocidade angular constante
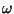
.
Figure 6:
Superposição de 2 rotações
|
|
O movimento de P em M pode ser descrito na forma
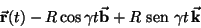 |
(1) |
onde
R é o raio da esfera,
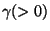
a velocidade angular de
P sobre M,
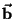
um vetor horizontal unitário no plano de M (Fig 6), e
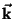
é o vetor unitário na direção de Z-positiva. Como
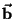
roda juntamente com a esfera, tem a forma
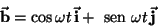 |
(2) |
onde
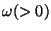
é a velocidade angular da esfera. Derivando a
equação 1 obtemos a velocidade
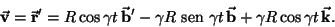 |
(3) |
Derivando mais uma vez obtemos a aceleração
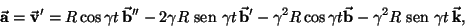 |
(4) |
onde por 2
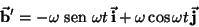 |
(5) |
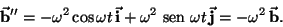 |
(6) |
De 1 vê-se que a soma dos últimos dois termos em 3
é igual
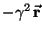
,
e 4 se torna
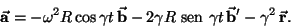 |
(7) |
O primeiro termo à direita é aceleração centrípeta causada pela
rotação
da esfera, e o último termo é a aceleração centrípeta resultante
da rotação do ponto
P. O segundo termo denomina-se
aceleração de Coriolis
Exercício 9
Seja p um ponto numa circunferência que rola tangenciando dentro uma
outra circunferência com diâmetro o dobro do diâmetro menor. Identifique
em termos bem simples a imagem da curva traçada por p.
Resposta: p percorre um diâmetro da circunferência maior.
Exercício 10
Sejam
f(
t)=3
t2-2
t3 para
![$t \in [0,1]$](img55.gif)
,
e
- 1.
- Mostre que c é uma parametrização derivável do polígono
com vértices A,B,
C, e D.
- 2.
- Construa uma parametrização derivável do pentágono regular centrado em
(0,0), com uma vértice em (1,0).
Aldrovando Azeredo Araujo
1999-05-21
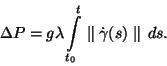
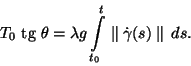
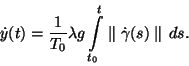
![\includegraphics[width=0.80\textwidth]{cat.eps}](img2.gif)
![\includegraphics[width=0.60\textwidth]{trac.eps}](img17.gif)
![\includegraphics[width=0.80\textwidth]{toy.eps}](img24.gif)
![\includegraphics[width=0.90\textwidth]{agn.eps}](img26.gif)
![\includegraphics[width=0.70\textwidth]{corio1.eps}](img34.gif)
![\includegraphics[width=0.70\textwidth]{corio2.eps}](img42.gif)
![\begin{displaymath}c(t)=\begin{cases}
(1-f(t))A + f(t)B & \quad \text{para} \qu...
...t-3))D +f(t-3)A &\quad\text{para}\quad t \in [3,4]
\end{cases}\end{displaymath}](img56.gif)