Lista III
Cálculo C
Exercício 1
Calcule os seguintes limites:
- 1.
-
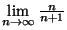
- 2.
-
 .
.
- 3.
-
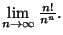
Exercício 2
Encontre os planos tangentes às superfícies nos pontos indicados:
- 1.
-
S definida pela equação
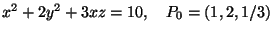
- 2.
-
S gráfico de

Exercício 3
Suponha que uma montanha tenha a forma de um parabolóide elítico de
equação
z=c-ax2-by2,
onde
a,
b e
c são constantes positivas e
x e
y são as direções leste-oeste e norte-sul.
No ponto (1,1) qual a direção para a qual a altura aumenta mais rapidamente?
Se uma pedra fosse solta em
(1,1,
c-
a-
b) qual a direção que começaria a rolar?
Exercício 4
Suponha que uma partícula seja ejetada de uma superfície de
equação
x2+
y2-
z2=1 do ponto
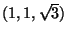
na direção da normal
que aponta para o plano
XY, com velocidade 10
m/
s. Determine quando
e onde a partícula encontrará o plano
XY.
Exercício 5
Um barco se move na direção norte-leste com velocidade escalar 20 km/h. Assuma que
a temperatura decresce
a uma taxa de 0.2oC/km na direção norte e 0.3oC/km na direção leste.
Qual é a taxa de variação da temperatura observada pelo barco?
Exercício 6 (Método do
steepest descent)
Suponhamos que estejamos interessados
em encontrar a solução de
f(x,y,z)=0.
Seja então
P0 uma primeira aproximação. Então se
f(
P0)=
c0> 0podemos nos aproximar da solução escolhendo uma direção na qual
f decresça, de fato
aquela que
f decresça mais rapidamente seria a ideal. Isto nos sugere
escolher
e tomando
h pequeno podemos tomar como segunda aproximaç ão
o processo continua até termos
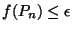
.
Aplique este método conhecido como método do gradiente descendente para
encontrar a solução de

Sugestão:Aplique o método para a função:
f(x,y,z)=(2x+3y+4z-5)2+(x2+y2+z2-7)2+(xyz-4)2.
Exercício 7
Seja
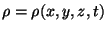
a densidade de um fluido em movimento que se desloca
com a seguinte velocidade
V(x,y,z,t)
isto é
V denota a velocidade da partícula do fluido que no instante
t estava em
(
x,
y,
z). Determine
e explique sua resposta através de um raciocínio físico e geométrico.
Exercício 8
Uma partícula desliza sem frição ao longo da hélice representada
pelas
equações paramétricas:

Se a partícula começa no ponto que corresponde a
z=
z0>0, então quando ela atinge a
altura
z sua velocidade é dada por
- 1.
- Encontre o comprimento da parte da hélice entre os plano z=z0 e z=z1com
0< z1<z0.
- 2.
- Calcule o tempo T0 que leva para a partícula alcançar o plano z=0.
Exercício 11
Seja
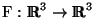
um campo conservativo
Uma curva
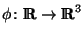
denomina-se
quase-Newtoniana se existem constantes
mi, chamadas suas componentes de massa tais que
para cada
i=1,2,3. Isto é, relativamente à direção
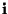
,
ela se comporta como
se tivesse massa
mi.
Defina sua
energia cinética
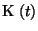
e sua
energia potencial
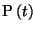
no tempo
t por

Prove que a lei de conservação de energia é válida
para partículas quase-Newtonianas,
isto é,
 .
.
Sugestão: Derive
 .
.
Exercício 12
Encontre as expressões em coordenadas cilíndricas para o divergente
e o rotacional
Exercício 13
Definimos o
operador de Laplace
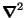
(ou
Laplaciano), que opera sobre funções escalares
f, como o divergente do gradiente:
Determine a expressão em coordenadas cilíndricas para o
Laplaciano.
Exercício 14
Mostre que se um campo é conservativo, então não
admite linhas de campo fechadas (ou trajetórias fechadas) isto é,
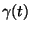
tal que
com
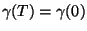
e
T>0. Uma tal trajetória denomina-se periódica.
Ver figura 1 abaixo.
Figure 1:
Campo conservativo
|
|
Aldrovando Azeredo Araujo
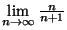
 .
.
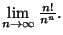



![]() .
.
![]() .
.