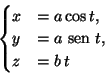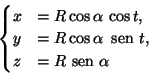Lista IV
Cálculo C
Exercício 2
Encontre a área da superfície lateral do cilindro
parabólico
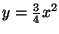
limitado pelos planos
z=0,
x=0,
z=
x,
y=6.
Exercício 3
Encontre a massa do fio de arame colocado sobre a elipse
se a densidade linear decada ponto é
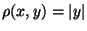
.
Exercício 4
Determine as coordenadas do centro de gravidade
do meio arco da ciclóide da letra (b) do exercício 1.
Exercício 5
Determine a força exercida por uma massa M distribuida com densidade uniforme sobre o círculo
x2+y2=a2, z=0 sobre uma massa m colocada no ponto
P=(0,0,b).
Exercício 6
Calcule as seguintes integrais de linha:
- 1.
-
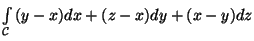 ,
onde
,
onde
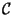 é uma
volta da hélice:
é uma
volta da hélice:
percorrida na direção do aumento do parâmetro.
- 2.
-
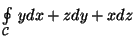 ,
onde
,
onde
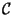 é o
círculo:
é o
círculo:
Exercício 7
Seja
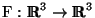
um campo de forças e
![$\gamma\colon [a,b]\rightarrow \ensuremath {\ensuremath{ \hbox{\matii R}}^3 } $](img20.gif)
uma curva parametrizada tal que
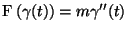
.
Mostre que o trabalho
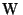
realizado pelo campo ao mover uma partícula de massa
m ao longo de
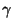
de
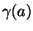
até
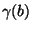
é
onde
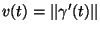
.
Deste modo o trabalho realizado corresponde a variação da
energia cinética da partícula.
Exercício 8
Um homem de 160 lb carrega uma lata de tinta que pesa 25 lb
para cima via uma escada em espiral que cerca um silo de raio 20 ft.
Se o silo tem 90 ft de altura e o homem faz três voltas completas,
determine o trabalho realizado pelo homem
contra a gravidade.
Exercício 9
Um arame tem a forma da curva obtida como interseção da porção
da esfera
com o plano
x-y+2z=1.
sabendo-se que a densidade em cada ponto do arame é dada por
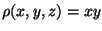
,
calcule a massa total do arame.
Exercício 10
Um tanque na forma de um cone invertido tem 10m de altura e 10m de
diâmtro no topo. Está com água até a altura 5m. Qual o trabalho
realizado pra se
bombear água de um orifício circular na base de área A até
preencher o tanque?
Exercício 11
Qual é o valor da integral de um campo gradiente ao longo de uma curva fechada?
Exercício 12
Um ciclista sobe de bicicleta uma montanha pelo caminho
mostrado na figura 1. Ele faz uma revolução completa ao redor da montanha
para alcançar o topo com ângulo de subida sempre constante. Ao longo do caminho
ele exerce uma força descrita pelo campo vetorial
Qual é o trabalho realizado pelo ciclista para subir de
A a
B.
Figure 1:
Ciclista subindo a ladeira
|
|
Exercício 13
Deseja-se construir uma peça de zinco que tem a forma da superfície
do cilindro
x2+y2=4
comprendida entre os planos
z=0 e
x+
y+
z=2 com
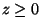
.
Se o
metro quadrado de zinco custa
M reais, calcule o preço total da peça.
Exercício 15
Calcule o volume de líquido que passa através da curva
fechada
x2+y2=1
pelo campo de velocidades do líquido cuja densidade é
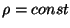
dado por
Aldrovando Azeredo Araujo
 onde
onde
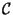 é o contorno do
quadrado |x|+|y|=a (a>0).
é o contorno do
quadrado |x|+|y|=a (a>0).
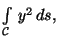 onde
onde
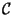 é
o primeiro arco da ciclóide
é
o primeiro arco da ciclóide
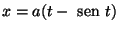 ,
,
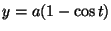 .
.
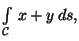 onde
onde
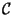 é
é o laço da direita da leminescata
é
é o laço da direita da leminescata
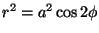 .
.