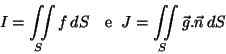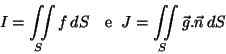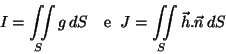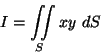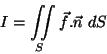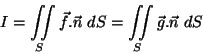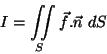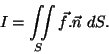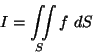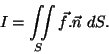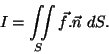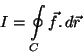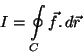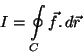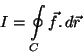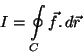Lista V
Cálculo C
Exercício 1
Calcule
sendo
S a porção do parabolóide
z=
x2+
y2, entre os
planos
z=0 e
z=3 (face externa), e
Exercício 2
Determine
nos seguintes casos:
- 1.
-
g(x,y,z)=xy,
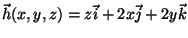 e S/'e a porção do plano
x+y+z=5 no
e S/'e a porção do plano
x+y+z=5 no
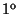 octante , com a normal apontando para fora
do tetraedro de vértices
octante , com a normal apontando para fora
do tetraedro de vértices
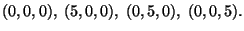
- 2.
-
g(x,y,z)=xyez,
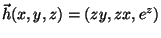 e S é a face externa da porção do cilindro x2+y2=3 entre os planos
z=1 e z=2.
e S é a face externa da porção do cilindro x2+y2=3 entre os planos
z=1 e z=2.
Exercício 3
Determine
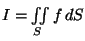
sendo
e
S a porção da superfície
y=
x2 entre os planos
x=0,
x=1,
z=0 e
z=2.
Exercício 4
Dada a superfície
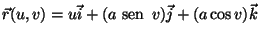
com
a>0,
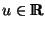
,
![$v\in[0,2\pi]$](img15.gif)
,
determine a área da porção
desta superfície compreendida entre os planos
x=0 e
x=3. Faça um esboço da superfície.
Exercício 5
Calcule
sendo
S a porção do cone
-
x2+
z2=
y2 entre os
planos
z=1 e
z=2.
Exercício 6
Uma lâmina tem a forma da porção
do plano
x+
y+
z=5 interior ao cilindro
x2+
y2=9 e contida no
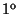
octante.
- 1.
- Determine a área da lâmina.
- 2.
- Se a densidade em cada ponto é proporcional
à soma das distâncias do ponto aos planos coordenados, determine a
massa da lâmina e as coordenadas do centro de massa.
- 3.
- Nas condições de (b), determine
a momento de inércia em relação a cada dos um dos eixos coordenados.
Exercício 7
Determinar a área de
S:
- 1.
- Se S é a superfície
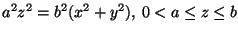 .
.
- 2.
- Se S é a porção da esfera
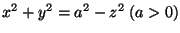 interior
ao cilindro
x2+y2=ay.
interior
ao cilindro
x2+y2=ay.
- 3.
- Se S é a porção do cone
z2=3(x2+y2) entre o plano z=0 e o parabolóide z=x2+y2.
- 4.
- Se S é a porção do parabolóide
2z=x2+y2 entre o plano z=0
e a esfera
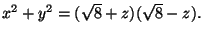
Exercício 8
Calcule
sendo :
- 1.
- S o hemisfério superior da esfera
x2+y2+z2=4 (face interna) e
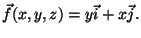
- 2.
- S a superfície externa do cubo
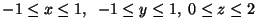 e
e
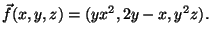
- 3.
- S a face externa da porção do cone
x2/4+y2/4-z2/9=0 compreendida entre os planos z=0 e z=3 com
- 4.
- S o elipsóide
e
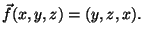
- 5.
- S a face interna da superfície que delimita o sólido cujas faces estão
nos planos x=3/2, x=-3/2, y=5/2, y=-5/2, e no elipsóide
x2/4+y2/9+z2/16=1 e
Exercício 9
Sejam
S a esfera
x2+
y2+
z2=
a2 (
a>0) e
e
Mostre que
se
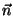
é o mesmo nas duas integrais.
Exercício 10
Seja
S a porção do plano
z-
y=0 interior ao cilindro
(
y-1)
2+
x2=1.
Se um fluido de densidade
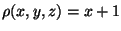
e velocidade
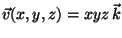
atravessa
S,
determine a massa de fluido que passa através de
S por unidade de tempo.
Exercício 11
Sejam
T o sólido limitado pelos planos
x=0,
y=0 e
z=0, pela esfera
x2+
y2+
z2=25 e pelo cilindro
x2+
y2=13, e
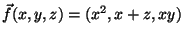
.
Determine
onde
S é a superfície delimitante de
T (face externa).
Exercício 12
Seja
T o sólido delimitado pela esfera
x2+
y2+
z2=9 e pelo parabolóide
z=
x2+
y2. Se
S é a superfície que limita
T, e
determine
Considere as duas possibilidades.
Exercício 13
Uma lâmina tem a forma da porção da superfície
comprendida entre os palnos
z=1 e
z=2.
- 1.
- Determine a área da lâmina.
- 2.
- Se a densidade em cada ponto é inversamente proporcional ao quadrado
da distância do ponto ao plano xy, determine a massa da lâmina.
Exercício 14
Uma lâmina tem a forma da superfície
z=(
x2+
y2)
3/2,
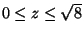
.
Se a densidade em cada ponto é proporcional ao quadrado
da distância do ponto ao eixo
z, determine a massa da lâmina.
Exercício 15
Sendo
S a porção do parabolóide
y=3-(
x2+
y2) tal que
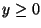
,
calcule
nos seguintes casos:
- 1.
-
f(x,y,z)=x2+z2+1.
- 2.
-
f(x,y,z)=3y
Exercício 16
Seja
T a porção do cilindro de raio 1, e com eixo coincidente
com o eixo
z,
interior à esfera
x2+
y2+
z2=9
2. Se
S é a superfície que
delimita
T (face externa) e
determine
Exercício 17
Sendo
S a superfície externa do sólido no
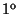
octante limitado por
x=0,
y=0,
z=0,
z=3 e
x2+
y2=1, e
determine
Exercício 18
Determine o volume do sólido limitado pelas
esferas de raios 1 e 2 (centradas na origem) e pelo cone
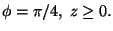
Exercício 19
Determine o volume do sólido limitado pelos
cones
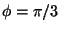
e
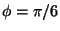
e pelos planos
z=1 e
z=5.
Exercício 20
Determine o volume do sólido limitado pela
esfera
x2+y2+z2=1 e pelo cone
z2=x2+y2
(considere as duas possibilidades).
Exercício 21
Sejam
S a porção do parabolóide
z=4-
x2-
y2 situada no
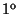
octante e
C o bordo de
S percorrido de (0,0,4)a (2,0,0) a (0,2,0) a (0,0,4). Sendo
determinar
Exercício 22
Calcule
onde
e
C é a curva
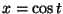
,
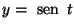
,
z=1 (
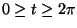
).
Exercício 23
Determine
sendo
C o contorno da porção do plano
6
x+3
y+2
z=24
contida no
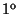
octante, percorrido no sentido de (4,0,0)a (0,8,0) a (0,0,12) a (4,0,0) e
Exercício 24
Determine
sendo
C o contorno da porção do cone
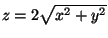
situada na região
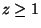
,
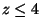
,
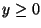
,
percorrido de
(1/2,0,1) a
(-1/2,0,1)a (-2,0,4) a (2,0,4) a (1/2,0,1) e
Exercício 25
Sendo
e
C a curva contida no cilindro
x2+
y2=1 como no desenho a seguir,
Figure 1:
Curva relativa ao ex.26
|
|
determine
- 1.
- diretamente
- 2.
- usando o teorema de Stokes.
Exercício 26
Determine
sendo
C o contorno a seguir esquematizado e
Figure 2:
Curva relativa ao ex.27
|
|
Aldrovando Azeredo Araujo