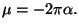Cálculo C

Exercício 1 No começo do século XIX Jean Baptiste Biot e Fèlix Savart anunciaram que um fio conduzindo uma corrente elétrica gera um campo magnético cujas linhas de fluxo são círculos no plano ortogonal ao fio, centrados no fio, de intensidade inversamente proporcional à distância ao fio e sentido determinado pela regra da mão direita.Usando esta informação faça:

1.

Assuma que o fio está localizado sobre o eixo z com a corrente no sentido negativo de z. Suponha que a densidade de corrente ( $J=\rho \vec{v}$ ) seja:

$\begin{displaymath}\vec{J}=(0,0,J_3).\end{displaymath}$

Determine o campo magnético.

$\begin{displaymath}\vec{B}=\frac{\alpha J_3}{x^2+y^2}(y,-x,0)\end{displaymath}$

onde $\alpha=$ const dependendo do meio.

2.

Se S é uma superfície limitada com fronteira uma curva fechada $\partial S$ em $\ensuremath {\ensuremath{ \hbox{\matii R}}} ^3$ então determine o trabalho que o campo magnético B realiza ao mover uma partícula ao longo de $\partial S$

$\begin{displaymath}\oint\limits_{\partial S} \alpha J_3 \frac{ydx-xdy}{x^2+y^2}=\begin{cases} &-2\alpha \pi J_3\\ & 0 \end{cases}\end{displaymath}$

Se você calculou corretamente poderá concluir que o trabalho realizado pelo campo magnético é igual a

$\begin{displaymath}(2\pi\alpha)\times \text{fluxo de $\vec{J}$ atrav\'es de $S$}\end{displaymath}$

3.

Suponha que

$\begin{displaymath}\vec{J}=(J_1,J_2,J_3),\quad \vec{B}=(B_1,B_2,B_3).\end{displaymath}$

Use a informação sobre o trabalho obtida acima e o teorema de Stokes para concluir que

$\begin{displaymath}\nabla \times \vec{B}=\mu \vec{J}.\end{displaymath}$

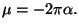
onde $\mu=-2\pi\alpha.$

Solução:

Já sabemos que:

$\begin{displaymath}\oint\limits_{\partial S} \vec{B}\centerdot ds= -2\pi\alpha \int\limits_S \vec{J}\centerdot dS\end{displaymath}$

Agora aplique Stokes e conclua que

$\begin{displaymath}\int\limits_S \nabla\times \vec{B}\centerdot dS= \int\limits_S \mu \vec{J}\centerdot dS.\end{displaymath}$

Como S é arbitrária conclua o resultado.

Exercício 2 Em 1831 Michael Faraday descobriu que movendo um campo magnético ao redor de um fio uma corrente elétrica podia ser produzida no fio . Seja

$\begin{displaymath}\vec{B}=\vec{B}(x,y,z,t)\end{displaymath}$

um campo magnético que varia no tempo. A característica fundamental do campo magnético é que suas linhas de fluxo são curvas fechadas e que portanto

$\begin{displaymath}\nabla\centerdot \vec{B}=0,\end{displaymath}$

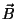
isto é que $\vec{B}$ é incompressível.

1.

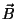Faraday afirmou que o trabalho realizado pela força eletromotiva E ao mover uma partícula ao longo de $\partial S$ é diretamente proporcional à variação do fluxo de $\vec{B}$ sobre S. Traduza isto em termos matemáticos.

2.

Usando como constante de proporcionalidade na fórmula encontrada igual a -1 e o teorema de Stokes conclua que:

$\begin{displaymath}\nabla\times E+\frac{\partial \vec{B}}{\partial t}=0.\end{displaymath}$

Solução:

A fórmula a ser encontrada é:

$\begin{displaymath}\oint\limits_{\partial S} \vec{E}\centerdot ds=\beta \frac{\partial} {\partial t} \int\limits_S \vec{B}\centerdot dS.\end{displaymath}$

Usando Stokes obtemos

$\begin{displaymath}\oint\limits_{\partial S} \vec{E}\centerdot ds=\int\limits_S ... ...centerdot dS=-\int\limits_S \frac{\partial \vec{B}}{\partial t}\end{displaymath}$

e usando que S é arbitrária conclua o resultado.