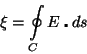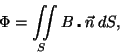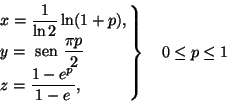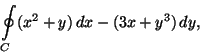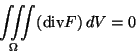Cálculo C
Lista 7
Exercício 1
Encontre as áreas das superfícies:
- 1.
- S o helicóide definido pela parametrização:
com
 ,
,
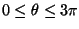
- 2.
- S é o toro representado parametricamente via:

com
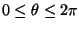 e
e
 e R>1.
e R>1.
Exercício 2
Encontre a área da região limitada por um arco de ciclóide
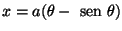
,
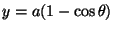
,
onde
a>0 e
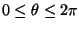
e o eixo dos
x.
Exercício 3
Determine
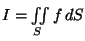
sendo
e
S a porção da superfície
y=
x2 entre os planos
x=0,
x=1,
z=0 e
z=2.
Os próximos dois exercícios tratam do significado do rotacional.
Imagine o campo representando um campo de velocidades de um fluido. Então
quando o rotacional é diferente do vetor nulo, se colocassemos pás
acopladas a um eixo,
dispostas como em um catavento sobre o ponto com o eixo na direção do
rotacional observaríamos estas pás girarem ao líquido se locomover
segundo a trajetória daquele ponto.
Exercício 4
Suponha que a água está fluindo em círculos segundo a lei:
em um ponto (
x,
y,
z) no tempo
t tem coordenadas
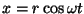
,
 z
z=
z, onde
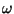
é a velocidade angular que supomos
constante. Determine o campo, verifique que este campo representa
aproximadamente o movimento
circular da água que está saindo de uma pia (por exemplo), e calcule o
rotacional deste campo. Interprete seu resultado.
Exercício 5
Faça o mesmo do exercício anterior
para os campos
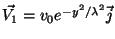
e
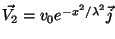
,
onde
v0
e
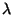
são constantes
. Faça um esboço das trajetórias dos campos. Interprete.
Exercício 6
A força eletromotiva
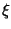
em um circuito
C é igual
a circulação do campo elétrico ao longo de
C:
Faraday descobriu que em um circuito estacionário uma força
eletromotiva é induzida pela variação do fluxo magnético. Isto é
onde
e
S é uma superfície que tem como fronteira
C. Use o teorema
de Stokes para provar que
que é uma das equações de Maxwell.
Exercício 7
Determine o valor de
onde
e
C é o caminho descrito por
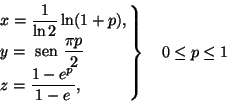 |
(1) |
do (0,0,0) até (1,1,1).
Exercício 8
Neste exerçício provaremos o seguinte teorema:
Seja
G um campo no
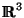
tal que
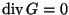
então existe
H tal que
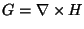
.
- 1.
- Mostre que
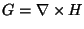 implica que div G=0.
implica que div G=0.
- 2.
- Para mostrar que div G=0 implica que podemos escrever
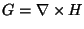 defina H por:
defina H por:

onde x0 e y0 são constantes arbitrárias. Mostre
que
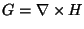 .
.
Exercício 9
Calcule as seguntes integrais:
- 1.
-
onde C é o quadrado com vértices
(0,0), (2,0), (2,2), (0,2) no sentido anti-horário.
- 2.
-
onde C é a elipse
x2+4y2=4 considerada no sentido anti-horário.
- 3.
-
onde
 e S é o elipsóide
e S é o elipsóide
x2+4y2+9z2=36
com a normal escolhida para fora.
Exercício 10
Suponha que
F seja tangente a uma superfície
S fechada
em cada um de seus pontos e que
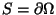
.
Prove que
Exercício 11
Seja
S a superfície da esfera unitária. Seja
F um campo
vetorial
e
Fr sua componente radial. Prove que
Exercício 12
Seja
S a porção do plano
z-
y=0 interior ao cilindro
(
y-1)
2+
x2=1.
Se um fluido de densidade
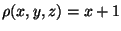
e velocidade
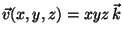
atravessa
S,
determine a massa de fluido que passa através de
S por unidade de tempo.
Exercício 13
Para uma distribuição de cargas estacionária e distribuição
de corrente com divergente zero, os campos elétrico e magnético
satisfazem:
Aqui
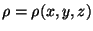
e
J(
x,
y,
z) são assumidas conhecidas.
A radiação produzida pelos campos através de uma superfície
S é determinada
pelo campo densidade de fluxo de radiação
, chamado o campo de
Poynting,
- 1.
- Se S é uma superfície fechada, mostre que o fluxo de radiação
através de S dado pelos campos acima é
onde V é a região delimitada por S.
- 2.
- Exemplos de tais campos são
Encontre o fluxo do campo de Poyning através do hemisfério
 da esfera
x2+y2+z2=25 com a normal apontando para a parte positiva do eixo y.
da esfera
x2+y2+z2=25 com a normal apontando para a parte positiva do eixo y.
Aldrovando Azeredo Araujo
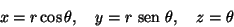
 ,
,
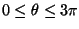

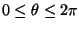 e
e
 e R>1.
e R>1.