Application of Fourier Series to Differential Equations
 



Application of Fourier Series to Differential Equations

Since the beginning Fourier himself was interested to find a powerful tool to be used in solving differential equations. Therefore, it is of no surprise that we discuss in this page, the application of Fourier series differential equations. We will only discuss the equations of the form

y(n) + an-1y(n-1) + ........+ a1y' + a0 y = f(x),

where f(x) is a $2\pi$-periodic function.

Note that we will need the complex form of Fourier series of a periodic function. Let us define this object first:

Definition. Let f(x) be 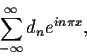$2\pi$-periodic. The complex Fourier series of f(x) is

\begin{displaymath}\sum_{-\infty}^{\infty} d_n e^{in\pi x},\end{displaymath}

where

\begin{displaymath}d_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x)e^{-in\pi x} dx.\end{displaymath}

We will use the notation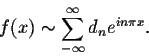

\begin{displaymath}f(x) \sim \sum_{-\infty}^{\infty} d_n e^{in\pi x}.\end{displaymath}

If you wonder about the existence of a relationship between the real Fourier coefficients and the complex ones, the next theorem answers that worry.

Theoreme. Let f(x) be 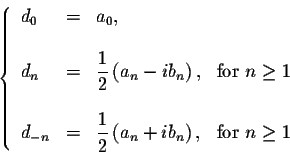$2\pi$-periodic. Consider the real Fourier coefficients $\{a_n\}$ and $\{b_n\}$ of f(x), as well as the complex Fourier coefficients $\{d_n\}$. We have

\begin{displaymath}\left\{\begin{array}{lcll} d_0 &=& a_0,\\ &&\\ d_n &=& \dis... ...n + i b_n \right),&\mbox{for $n \geq 1$}\\ \end{array}\right. \end{displaymath}

The proof is based on Euler's formula for the complex exponential function.

Remark. When f(x) is 2L-periodic, then the complex Fourier series will be defined as before where

\begin{displaymath}d_n = \frac{1}{2c} \int_{-c}^{c} f(x) e^{ \displaystyle -i(n\pi x /c)} dx,\end{displaymath}

for any $n = 0, \pm 1, \pm 2,...$.

Example. Let f(x) = x, for $x \in ]-1,1[$ and f(x+2) = f(x). Find its complex Fourier coefficients $\{d_n\}$.
Answer. We have d0 = 0 and

\begin{displaymath}d_n = \frac{1}{2} \int_{-1}^{1} xe^{ \displaystyle-in\pi x} dx.\end{displaymath}

Easy calculations give

\begin{displaymath}d_n = \frac{-1}{2} \left[ \frac{e^{ \displaystyle in\pi}}{in\... ...n\pi)^2} + \frac{e^{ \displaystyle -in\pi}}{(in\pi)^2} \right].\end{displaymath}

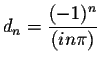Since $e^{ \displaystyle i\pi} = e^{ \displaystyle -i\pi} = -1$, we get $\displaystyle d_n = \frac{(-1)^n}{(in\pi)}$. Consequently

\begin{displaymath}f(x) \sim \sum_{n=1}^{ \displaystyle \infty} \frac{(-1)^{ \di... ...^{ \displaystyle in\pi x} - e^{ \displaystyle -in\pi x} \Bigg].\end{displaymath}

Back to our original problem. In order to apply the Fourier technique to differential equations, we will need to have a result linking the complex coefficients of a function with its derivative. We have:

Theorem. Let f(x) be 2L-periodic. Assume that f(x) is differentiable. If

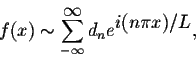
\begin{displaymath}f(x) \sim \sum_{-\infty}^{ \displaystyle \infty} d_n e^{ \displaystyle i(n\pi x)/L},\end{displaymath}

then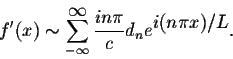

\begin{displaymath}f'(x) \sim \sum_{-\infty}^{ \displaystyle \infty} \frac{in\pi}{c} d_n e^{ \displaystyle i(n\pi x)/L}.\end{displaymath}

Example. Find the periodic solutions of the differential equation

y' + 2y = f(x),

where f(x) is a $2\pi$-periodic function.
Answer. Set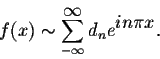

\begin{displaymath}f(x) \sim \sum_{-\infty}^{ \displaystyle \infty} d_n e^{ \displaystyle in\pi x}.\end{displaymath}

Let y be any 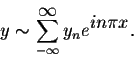$2\pi$-periodic solution of the differential equation. Assume

\begin{displaymath}y \sim \sum_{-\infty}^{ \displaystyle \infty} y_n e^{ \displaystyle in\pi x}.\end{displaymath}

Then, from the differential equation, we get

\begin{displaymath}in y_n + 2y_n = f_n,\;\;\mbox{for any $n$}.\end{displaymath}

Hence

\begin{displaymath}y_n = \frac{1}{2 + in} f_n,\;\;\mbox{for any $n$}.\end{displaymath}

Therefore, we have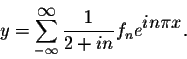

\begin{displaymath}y = \sum_{-\infty}^{ \displaystyle \infty} \frac{1}{2 + in} f_n e^{ \displaystyle in\pi x}.\end{displaymath}

Example. Find the periodic solutions of the differential equation

\begin{displaymath}y'' + 2y' + y = \sin(x).\end{displaymath}

Answer. Because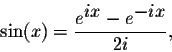

\begin{displaymath}\sin(x) = \frac{e^{ \displaystyle ix} - e^{ \displaystyle -ix}}{2i},\end{displaymath}

we get 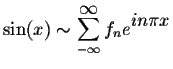$\sin(x) \sim \displaystyle \sum_{-\infty}^{ \displaystyle \infty} f_n e^{ \displaystyle in\pi x}$ with

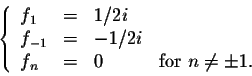
\begin{displaymath}\left\{\begin{array}{lcll} f_1 &=& 1/2i\\ f_{-1} &=& -1/2i\\ f_n &=& 0&\mbox{for $n \neq \pm1$.}\\ \end{array}\right.\end{displaymath}

Let y be a periodic solution of the differential equation. If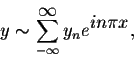

\begin{displaymath}y \sim \sum_{-\infty}^{ \displaystyle \infty} y_n e^{ \displaystyle in\pi x},\end{displaymath}

then $\Big[(in)^2 + 2(in) + 1\Big]y_n = f_n$. Hence

\begin{displaymath}y_1 = y_{-1} = -\frac{1}{4}, \;\;\; \mbox{and}\;\;\; y_n = 0 \;\;\;\mbox{otherwise}.\end{displaymath}

Therefore, the differential equation has only one periodic solution

\begin{displaymath}y = -\frac{1}{4} e^{ \displaystyle ix} -\frac{1}{4}e^{ \displaystyle -ix} = -\frac{1}{2}\cos(x).\end{displaymath}

The most important result may be stated as:

Theoreme. Consider the differential equation

\begin{displaymath}y^{ \displaystyle (m)} + a_{m-1}y^{ \displaystyle (m-1)} + ........+ a_1y' + a_0 y = f(x),\end{displaymath}

where f(x) is a 2c-periodic function. Assume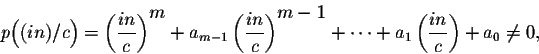

\begin{displaymath}p\Big((in)/c\Big) = \left(\frac{in}{c}\right)^{ \displaystyle... ...style m-1} + \cdots+ a_1\left(\frac{in}{c}\right) + a_0 \neq 0,\end{displaymath}

for $n = 0, \pm1,\pm2,\cdots$. Then the differential equations has one 2c-periodic solution given by

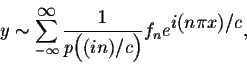
\begin{displaymath}y \sim \sum_{-\infty}^{ \displaystyle \infty} \frac{1}{p\Big((in)/c\Big)} f_n e^{ \displaystyle i(n\pi x)/c},\end{displaymath}

where

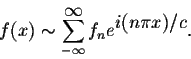
\begin{displaymath}f(x) \sim \sum_{-\infty}^{ \displaystyle \infty} f_n e^{ \displaystyle i(n\pi x)/c}.\end{displaymath}