Lista VII

Cálculo D

Exercício 1   Calcule as raízes abaixo:

a) $(2\sqrt{3}-2i)^{1/2}$        b) (-4+4i)^1/5        c) $\sqrt[6]{64}$

Exercício 2   Resolva

a) z⁴+81=0        b) z⁵-2z⁴-z³+6z-4=0        c) z⁴+z²+1=0

Exercício 3   Prove que:

$$\cos \theta+\cos (\theta+\alpha)+\cos (\theta+2\alpha)+\cdots... ...text {\ sen }}\frac{1}{2}\alpha}\cos(\theta+\frac{1}{2}n\alpha)$$

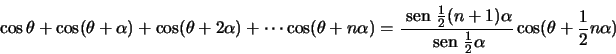
Exercício 4   Prove que

$$1+a\cos \theta +a^2\cos(2\theta)+a^3\cos(3\theta)+\cdots =\frac{1-a\cos \theta}{1-2a\cos \theta+a^2}.$$

Exercício 5   Exprima w na forma w=u(x,y)+i(v(x,y) para

a) w=z³+3z²                        b) $w=\frac{(z^2+1)}{2z}$

Exercício 6   Exprima w na forma w=w(z) para

a) w=x³-3xy²+2x+i(3x²y-y³+2y)

b) $w=\frac{-6(x^2+y^2)+2-x}{4(x^2+y^2)+1-4x}+i\frac{7y}{4(x^2+y^2)+1-4x}$

Exercício 7  

Ache f'(z) para as funções abaixo:

a) $f(z)={\text {\ sen }}x \cosh y-i\cos x{\text {\ senh }}y$

b) $f(z)=\cos x \cosh y-i{\text {\ sen }}x{\text {\ senh }}y$

c) f(z)=e^z

Exercício 8  

Ache as soluções e^z2=1

Exercício 9   Determine a imagem dos eixos coordenados e de linhas
paralelas a eles pela transformação $w={\text {\ sen }}z$.

Exercício 10   Mostre que a função $f(z)=A{\text {\ sen }}\lambda z+B\cos \lambda z$ satisfaz a equação diferencial:

$$\frac{d^2f}{dz^2}+\lambda^2 f=0.$$

Exercício 11   Mostre que se f(z) é qualquer função que satisfaz a equação diferencial:

$$\frac{d^2f}{dz^2}+\lambda^2 f=g(z)$$

então a função $f(z)+A{\text {\ sen }}\lambda z+B\cos \lambda z$, também a satisfaz.

Exercício 12   Ache todas as raízes de

$$\cosh z=1.$$

Exercício 13   Para cada uma das funções abaixo localize e classifique as singularidades:

a) $f(z)=\frac{z^2-3z}{z^2+2z+2}$            b) $f(z)=\frac{\ln (z+3i)}{z^2}$            c) $f(z)=\frac{\cos z}{(z+i)^3}$

Exercício 14   Mostre que as equações de Cauchy-Riemann se escrevem na forma polar como:

$$\frac{\partial u}{\partial r}=\frac{1}{r}\frac{\partial v}{\p... ...l v}{\partial r}=-\frac{1}{r}\frac{\partial u}{\partial \theta}$$

Exercício 15   Calcule:

a) $\lim\limits_{z\to 0}\frac{z^4}{2\cos z-2+z^2}$                     a) $\lim\limits_{z\to 0}\frac{120z-20z^3+z^5-120{\text {\ sen }}z}{\frac{1}{42}z^7}$

Exercício 16   Mostre que cada u(x,y) abaixo é harmônica e calcule sua conjugada harmônica

$$u(x,y)=e^{e^x\cos x}\cos(e^x{\text {\ sen }}y)$$

u(x,y)=x²-y²-2xy-2x+3y