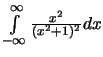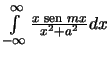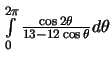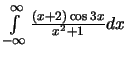Lista VIIICálculo D
Exercício 1
Calcule as integrais
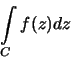
onde
a)
Resposta: 1
Resposta:
Resposta: -1
Resposta: 0
Resposta:
Resposta:
Resposta:
h)
Resposta:
Resposta: 0 se n é ímpar e
Exercício 2
Observe os modelos abaixo:
Para resolver a) fazemos:
Como 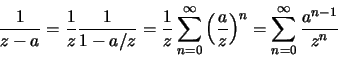
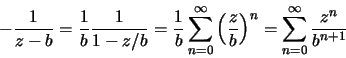
Logo 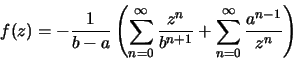
para a<|z|<b.
Para a parte b) usamos a mesma decomposição em frações parciais de a)
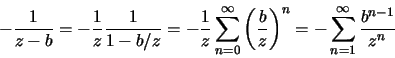
que vale para |z|>b. Como b>a o desenvolvimento de 1/(z-a) obtido em a) é válido para |z|>ae pode ser usado aqui. Assim, 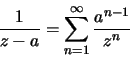
que vale para |z|>a e portanto para |z|>b. Portanto 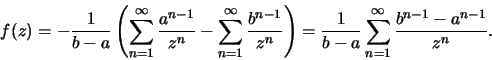
Note que o primeiro termo deste somatório se anula, pois b0-a0=0. Logo 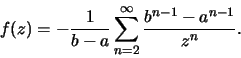
Para a letra c) podemos escrever,
onde 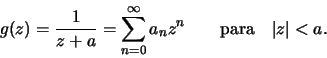
Por derivação obtemos para todo n=1,2,3.... Portanto como 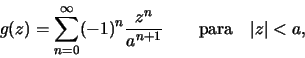
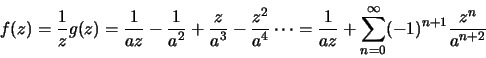
no domínio 0<|z|<1.
Resposta:
Exercício 3
Calcule
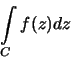
onde
a)
Resposta: 0
Resposta:
Exercício 4
Calcule as integrais reais;
a)
Resposta:
b)
Resposta:
c)
Resposta:
d)
Resposta:
Exercício 5
Determine as singularidades e calcule os resíduos:
a)
Resposta: z1=-1,
Res(f,z1)=2 e z2=-2 com
Res(f,z2)=-1.
|
 .
.