Series Solutions: Introduction

Throughout these pages I will assume that you are familiar with power series and the concept of the radius of convergence of a power series.

Let us consider the example of the second order differential equation

$\begin{displaymath}y''+4y=0,\quad y(0)=1,\ y'(0)=0.\end{displaymath}$

You probably already know that the solution is given by $y(t)=\cos(2t)$ ; recall that this function has as its Taylor series

$\begin{displaymath}\cos(2t)=1-\frac{2^2 t^2}{2!}+\frac{2^4 t^2}{4!}-\frac{2^6 t^6}{6!}+\ldots,\end{displaymath}$

and that this representation is valid for all $t\in\Bbb R$ .

Do you remember how to compute the Taylor series expansion for a given function?

If everything works out, then

$\begin{displaymath}y(t)=a_0+a_1\cdot t+a_2 \cdot t^2 + a_3\cdot t^3\ldots,\end{displaymath}$

where

$\begin{displaymath}a_n=\frac{y^{(n)}(0)}{n!}.\end{displaymath}$

Here y⁽ⁿ⁾(0) denotes the nth derivative of y at the point t=0.

What does this mean? To compute the Taylor series for the solution to our differential equation, we just have to compute its derivatives. Note that the initial conditions give us a head start: y(0)=1, so a₀=1. y'(0)=0, so a₁=0.

We can rewrite the differential equation as

y''=-4y,

so in particular

$\begin{displaymath}y''(0)=-4y(0)=-4\cdot 1=-4.\end{displaymath}$

Consequently a₂=-4/2!=-2. By now, we have figured out that the solution to our differential equation has as its second degree Taylor polynomial the function 1-2t².

Next we differentiate

y''=-4y

on both sides with respect to t, to obtain

y'''=-4y',

so in particular

y'''(0)=-4y'(0)=0,

yielding a₃=0.

We can continue in this fashion as long as we like: Differentiating

y'''=-4y'

yields

y⁽⁴⁾=-4y'',

in particular

$\begin{displaymath}y^{(4)}(0)=-4y''(0)=-4\cdot (-4)=16,\end{displaymath}$

so a₄=16/4!=2/3. At this point we have figured out that the solution to our differential equation has as its fourth degree Taylor polynomial the function

$\begin{displaymath}1-2t^2+\frac{2}{3}t^4.\end{displaymath}$

We expect that this Taylor polynomial is reasonably close to the solution y(t) of the differential equation, at least close to t=0. In the picture below, the solution $y(t)=\cos(2t)$ is drawn in red, while the power series approximation $f(t)=1-2t^2+\frac{2}{3}t^4$ is depicted in blue:

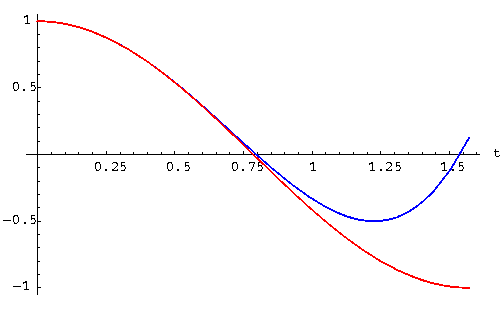
The method outlined works also in theory for non-linear differential equations, even though the computational effort usually becomes prohibitive after the first few steps. Let's consider the example

$\begin{displaymath}y''+\sin(y)=0,\quad y(0)=0,\ y'(0)=1.\end{displaymath}$

We try to find the Taylor polynomials for the solution, of the form

$\begin{displaymath}a_0+a_1\cdot t+a_2 \cdot t^2 + a_3\cdot t^3\ldots,\end{displaymath}$

where

$\begin{displaymath}a_n=\frac{y^{(n)}(0)}{n!}.\end{displaymath}$

The initial conditions yield a₀=0 and a₁=1. To find a₂, we rewrite the differential equation as

$\begin{displaymath}y''=-\sin(y),\end{displaymath}$

and plug in t=0:

$\begin{displaymath}y''(0)=-\sin(y(0))=-\sin(0)=0;\end{displaymath}$

consequently a₂=0.

Next we differentiate

$\begin{displaymath}y''=-\sin(y)\end{displaymath}$

on both sides with respect to t, to obtain

$\begin{displaymath}y'''=-\cos(y)\cdot y',\end{displaymath}$

so in particular

$\begin{displaymath}y'''(0)=-\cos(y(0))\cdot y'(0)=-\cos(0)\cdot 1=-1,\end{displaymath}$

yielding a₃=-1/3!=-1/6. Note that since we were differentiating with respect to t, we had to use the chain rule to find the derivative of the term $\sin(y(t))$ .

Let's continue a little bit longer: We differentiate

$\begin{displaymath}y'''=-\cos(y)\cdot y',\end{displaymath}$

to obtain

$\begin{displaymath}y^{(4)}=\sin(y)\cdot (y')^2-\cos(y)\cdot y''.\end{displaymath}$

Consequently y⁽⁴⁾(0)=0, and thus a₄=0.

Differentiating

$\begin{displaymath}y^{(4)}=\sin(y)\cdot (y')^2-\cos(y)\cdot y'' \end{displaymath}$

yields

$\begin{displaymath}y^{(5)}=\cos(y)\cdot (y')^3+\sin(y)\cdot 2(y')\cdot y''+\sin(y)\cdot y'\cdot y''-\cos(y)\cdot y'''.\end{displaymath}$

You can check that y⁽⁵⁾=y'(0)³-y'''(0)=1-(-1)=2 and thus a₅=2/5!.

The fifth degree Taylor polynomial approximation to the solution of our differential equation has the form

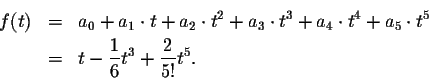
$\begin{eqnarray*}f(t)&=&a_0+a_1\cdot t+a_2 \cdot t^2 + a_3\cdot t^3+a_4\cdot t^4 +a_5 \cdot t^5\\ &=&t-\frac{1}{6}t^3+\frac{2}{5!}t^5. \end{eqnarray*}$

We again expect that this Taylor polynomial is reasonably close to the solution y(t) of the differential equation, at least close to t=0. In the picture below, the solution, as computed by a numerical method, is drawn in red, while the power series approximation $f(t)=t-\frac{1}{6}t^3+\frac{2}{5!}t^5$ is depicted in blue:

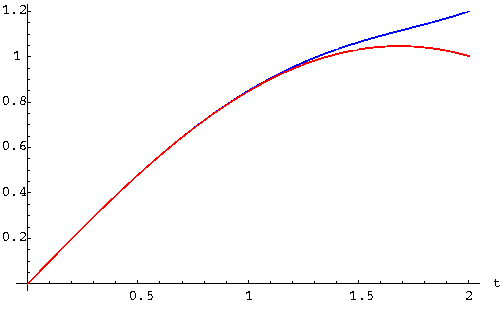
The next sections will develop an organized method to find power series solutions for second order linear differential equations. Here are a couple of examples to practice what you have learned so far:

Series Solutions: Introduction

Exercise 1:

Answer.

Exercise 2:

Answer.