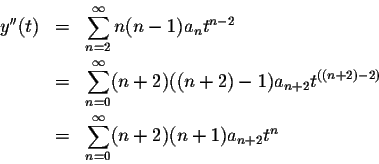Series Solutions: Taking Derivatives and Index Shifting

Throughout these pages I will assume that you are familiar with power series and the concept of the radius of convergence of a power series.

Given a power series

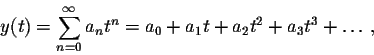
$\begin{displaymath}y(t)=\sum_{n=0}^\infty a_n t^n=a_0+a_1 t+a_2 t^2 +a_3 t^3+\ldots,\end{displaymath}$

we can find its derivative by differentiating term by term:

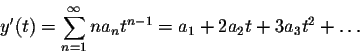
$\begin{displaymath}y'(t)=\sum_{n=1}^\infty n a_n t^{n-1}=a_1+2 a_2 t + 3 a_3 t^2+\ldots\end{displaymath}$

Here we used that the derivative of the term a_n tⁿ equals a_n n t^n-1. Note that the start of the summation changed from n=0 to n=1, since the constant term a₀ has 0 as its derivative.

The second derivative is computed similarly:

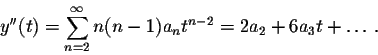
$\begin{displaymath}y''(t)=\sum_{n=2}^\infty n(n-1) a_n t^{n-2}=2 a_2 +6 a_3 t+\ldots.\end{displaymath}$

Taking the derivative of a power series does not change its radius of convergence, so $y(t), y'(t),y''(t),\dots$ will all have the same radius of convergence.

The rest of this section is devoted to "index shifting". Consider the example

$\begin{displaymath}\int_2^5 (x+1)^5\,dx.\end{displaymath}$

Using a simple substitution u=x+1, we can rewrite this integral as

$\begin{displaymath}\int_3^6 u^5 \,du,\end{displaymath}$

or changing the dummy variable u back to x, we get:

$\begin{displaymath}\int_2^5 (x+1)^5\,dx=\int_3^6 x^5\, dx.\end{displaymath}$

The expression (x+1) is "shifted down" by one unit to x, while the limits of integration are "shifted up" by one unit from 2 to 3, and 5 to 6.

Summation is just a special case of integration, so an analogous "index shifting" will work:

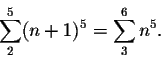
$\begin{displaymath}\sum_2^5 (n+1)^5=\sum_3^6 n^5.\end{displaymath}$

You should convince yourself that both of these expressions are indeed the same, by writing out explicitly the four terms of each of the two formulas!

Let's try this for our derivative formulas:

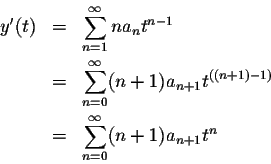
$\begin{eqnarray*}y'(t)&=&\sum_{n=1}^\infty n a_n t^{n-1}\\ &=&\sum_{n=0}^\infty... ..._{n+1} t^{((n+1)-1)}\\ &=&\sum_{n=0}^\infty (n+1) a_{n+1} t^{n} \end{eqnarray*}$

We shifted each occurrence of n in the expression up by one unit, while the limits of summation were shifted down by one unit, from 1 to 0, and from $\infty$ to $\infty-1=\infty$ .

You should once again convince yourself that the first and the last formula are indeed the same, by writing out explicitly the first few terms of each of the two formulas!

As a last example, let's shift the formula for the second derivative by 2 units:

$\begin{eqnarray*}y''(t)&=&\sum_{n=2}^\infty n(n-1) a_n t^{n-2}\\ &=&\sum_{n=0}^... ...2} t^{((n+2)-2)}\\ &=&\sum_{n=0}^\infty (n+2)(n+1)a_{n+2} t^{n} \end{eqnarray*}$

[Back]