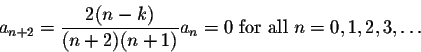Series Solutions: Hermite's Equation

Find the Hermite Polynomials of order 1 and 3.

Recall that the recurrence relations are given by

$\begin{displaymath}a_{n+2}= \frac{2(n-k)}{(n+2)(n+1)}a_n=0\mbox{ for all } n=0,1,2,3,\ldots\end{displaymath}$

We have to evaluate these coefficients for k=1 and k=3, with initial conditions a₀=0, a₁=1.

When k=1,

$\begin{displaymath}a_3=\frac{2(1-1)}{2\cdot 3} a_1=0.\end{displaymath}$

Consequently all odd coefficients other than a₁ will be zero. Since a₀=0, all even coefficients will be zero, too. Thus

H₁(t)=t.

When k=3,

$\begin{displaymath}a_3=\frac{2(1-3)}{2\cdot 3} a_1=-\frac{2}{3},\end{displaymath}$

and

$\begin{displaymath}a_5=\frac{2(3-3)}{4\cdot 5} a_3=0.\end{displaymath}$

Consequently all odd coefficients other than a₁ and a₃ will be zero. Since a₀=0, all even coefficients will be zero, too. Thus

$\begin{displaymath}H_3(t)=t-\frac{2}{3}t^3.\end{displaymath}$