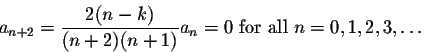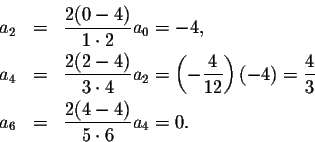Series Solutions: Hermite's Equation

Exercise 2:

Find the Hermite Polynomials of order 2, 4 and 6.

Answer.

Recall that the recurrence relations are given by

$\begin{displaymath}a_{n+2}= \frac{2(n-k)}{(n+2)(n+1)}a_n=0\mbox{ for all } n=0,1,2,3,\ldots\end{displaymath}$

We have to evaluate these coefficients for k=2, k=4 and k=6, with initial conditions a₀=1, a₁=0.

When k=2,

$\begin{displaymath}a_2=\frac{2(0-2)}{1\cdot 2} a_0=-2,\end{displaymath}$

while

$\begin{displaymath}a_4=\frac{2(2-2)}{3\cdot 4} a_2=0.\end{displaymath}$

Consequently all even coefficients other than a₂ will be zero. Since a₁=0, all odd coefficients will be zero, too. Thus

H₂(t)=1-2t².

When k=4,

$\begin{eqnarray*}a_2&=&\frac{2(0-4)}{1\cdot 2} a_0=-4,\\ a_4&=&\frac{2(2-4)}{3\... ...ft(-4\right)=\frac{4}{3}\\ a_6&=&\frac{2(4-4)}{5\cdot 6} a_4=0. \end{eqnarray*}$

Consequently all even coefficients other than a₂ and a₄ will be zero. Since a₁=0, all odd coefficients will be zero, too. Thus

$\begin{displaymath}H_4(t)=1-4t^2+\frac{4}{3}t^4.\end{displaymath}$

You can check that

$\begin{displaymath}H_6(t)=1 - 6\,{t^2} + 4\,{t^4} - {\frac{8}{15} t^6}.\end{displaymath}$

[Back] [Exercises]