More Examples on Series

Problem 1: Test for convergence

.

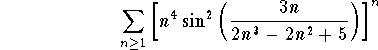Answer: Since we have a power n in the series, we will use the Root-Test. Set

.

We have

.

Since

,

and

,

we get

.

But,

.

Hence,

.

Therefore, by the Root-Test, the series

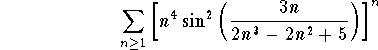
is divergent.

Problem 2: Test for convergence

.

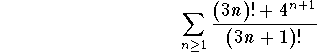Answer: We have

.

Hence, the series 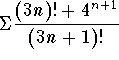converges, if and only if, both series 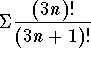and 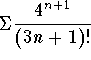are convergent. We have

.

Since

and the series is divergent (p-test), then using the Limit-Test, we conclude that the series 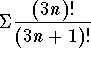is divergent. Therefore, the series

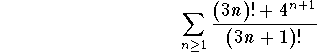
is divergent.

Problem 3: Test for convergence

.

Answer: We will use the Ratio-Test (try to use the Root-Test to see how difficult it is). Set

.

We have

.

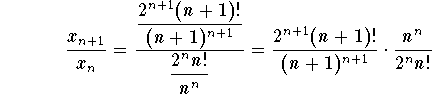Algebraic manipulations give

,

since

.

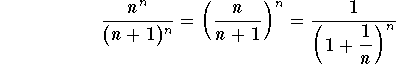Hence, we have

,

which implies

.

Since , we conclude, from the Ratio-Test, that the series

is convergent.

Problem 4: Determine whether the series

is convergent or divergent.

Answer: Consider the function

.

It is easy to check that f(x) is decreasing on . Hence, for any , we have for any ,

,

which implies

,

that is,

.

Using this inequality, we get

,

since

.

Since

,

we deduce that the partial sums associated to the series

are not bounded. Therefore, the series

is divergent.

Remark: Note that the proof given above is the proof of the Integral-Test. In other words, we may have just used to Integral-Test to get the conclusion. Also, the series given here is part of a type of series called Bertrand series defined as

.