 The Radius of Convergence
The Radius of Convergence The Radius of Convergence
The Radius of ConvergenceThe Ratio Test can be used to find out, for what values of x a given power series
![]()
converges. It works by comparing the given power series to the geometric series. Recall that the geometric series
![]()
is convergent exactly when -1<q<1.
Let's consider a series (no power yet!) and be patient for a couple of moments:
![]()
Suppose that all ![]() s are positive and that there is a q<1 so that
s are positive and that there is a q<1 so that
![]()
Then we know that ![]() ; we also know that
; we also know that ![]() ; in the next step we can recursively conclude that
; in the next step we can recursively conclude that
![]() ; in general we obtain
; in general we obtain
![]()
Thus we can conclude that the series under consideration converges:
![]()
The partial sums ![]() are all caught between the leftmost part of the inequality (0) and the rightmost part
are all caught between the leftmost part of the inequality (0) and the rightmost part 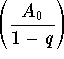 .
Since the partial sums are increasing, the series has no choice but to
converge!
.
Since the partial sums are increasing, the series has no choice but to
converge!
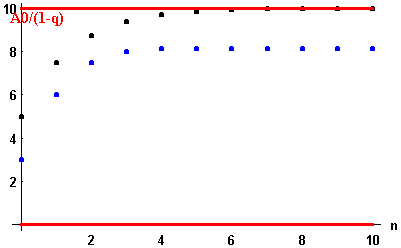
Maybe a picture helps. The series under consideration is depicted in blue; it is caught between 0 (in red) and the geometric series (in black), which itself is bounded by its limit (in red).
 |
Click here for the answer.