a)
![]()
![]()
![\begin{displaymath}y=1+ \sum\limits_{k=1}^\infty\frac{1}{[2\cdot 5\cdot 8\cdots
(3k-1)]k!}x^{3k}\end{displaymath}](images/img3.gif)
![\begin{displaymath}y_2= \sum\limits_{k=0}^\infty\frac{1}{[1\cdot 4\cdot 7\cdot \cdots (3k+1)
k!}]x^{3k+1}\end{displaymath}](images/img4.gif)
b)
![]()
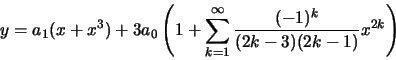
c)
![]()
![\begin{displaymath}y=a_1(x+\frac{8}{3}x^3)+
a_0\left[ 1+ 9x^2+\frac{15}{2}x^4+3\...
...ty
(-1)^k\frac{(2k-5)!(2k+1)}{2^{k-3}[k!(k-3)!]}x^{2k} \right]\end{displaymath}](images/img8.gif)
d)
![]()
![]()
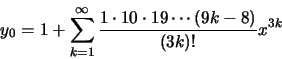
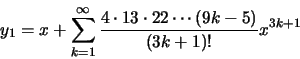
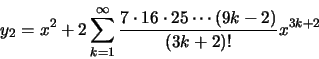
Cálculo D (E)
a)
![]()
![]()
![\begin{displaymath}y=1+ \sum\limits_{k=1}^\infty\frac{1}{[2\cdot 5\cdot 8\cdots
(3k-1)]k!}x^{3k}\end{displaymath}](images/img3.gif)
![\begin{displaymath}y_2= \sum\limits_{k=0}^\infty\frac{1}{[1\cdot 4\cdot 7\cdot \cdots (3k+1)
k!}]x^{3k+1}\end{displaymath}](images/img4.gif)
b)
![]()
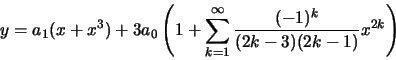
c)
![]()
![\begin{displaymath}y=a_1(x+\frac{8}{3}x^3)+
a_0\left[ 1+ 9x^2+\frac{15}{2}x^4+3\...
...ty
(-1)^k\frac{(2k-5)!(2k+1)}{2^{k-3}[k!(k-3)!]}x^{2k} \right]\end{displaymath}](images/img8.gif)
d)
![]()
![]()
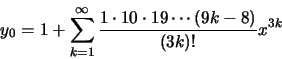
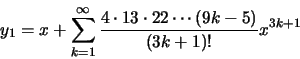
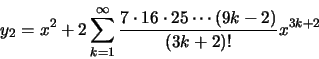
a)
b)
Solução:
c)
Solução:
![]() onde
onde