Um
compêndio de Scilab
Conteúdo
2. Instalando e executando Scilab
o Operadores
o Funções
o Constantes
o As linhas de comando
o Estrutura de dados
o Caracteres
o Salvando e carregando as variáveis
5. Matrizes
o Introduzindo Matrizes
o Somas
o Índices
o O operador :
o Geração de matrizes
o Concatenação
o Apagando linhas e colunas
o A inversa e a resolução de sistemas lineares
o Criando funções
o Controle de fluxo
o Algumas dicas de programação
o Debugando
7. Gráficos
o 2D
o 3D
9. Referências
 1. O que
é Scilab
1. O que
é Scilab
Scilab é um software de computação numérica, gratuito, desenvolvido inicialmente por pesquisadores do INRIA e atualmente mantido pelo Scilab Consortium . É similar ao Matlab, um clone. Scilab está formado por três componentes principais:
· um interpretador
· livrarias de funções (os procedimentos do Scilab)
· as rotinas de Fortran e C
Scilab se especializa na manipulação de matrizes (operações básicas, cálculo da transposta, inversa, etc.) e cálculo numérico computacional. Também possui um ambiente de programação aberto que permita aos usuários criar suas próprias funções e livrarias.
Para maior informação visite a página de Scilab:
 2.
Instalando e rodando Scilab
2.
Instalando e rodando Scilab
Antes que nada você deve fazer a descarga do software. Na seção de download da página do Scilab procure pela versão que corresponda a seu sistema operacional e clique em download (assumiremos que é Windows). Para facilitar a instalação é recomendado fazer a descarga do instalador. Terminada a descarga clique duas vezes no arquivo executável e siga as instruções para uma instalação completa.
Para executar Scilab clique duas vezes no atalho no menu principal de Windows.
 3.
Documentação e ajuda (Help)
3.
Documentação e ajuda (Help)
Para entender o uso de qualquer função clique em ? na barra de menu e procure pela função desejada.
 4. Scilab
elementar
4. Scilab
elementar
Operações
básicas
|
+
|
soma
|
|
-
|
subtração
|
|
*
|
produto
|
|
/
|
divisão
|
|
^
|
potência
|
|
'
|
transposta
|
Funções
básicas
sin, cos, tan, asin, acos, atan, abs, min, max, sqrt, sum
Por exemplo, entrando:
sin(0.5)
teremos como resultado:
ans =
0.4794255
Outro exemplo:
max(2, 3, abs(-5), sin(1))
ans =
5
Constantes
especiais
Algumas constantes usuais como, i (a unidade imaginária) (sqrt(-1)) ; o número e (base do logaritmo natural) e o número pi podem ser usadas com o formato
%pi %i %e
respectivamente. Também as constantes Booleanas representando true (verdadeiro) e false (falso)
%t %f
respectivamente.
A
linha de comando
Vários comandos podem ser colocados em uma mesma linha separados por comas:
A = [1 2 3], s = tan(%pi/4) + %e
A =
Um ponto e vírgula no fim da linha impedem que se exiba a saída do resultado (não "ecoa"):
A = [1 2 3]; s = tan(%pi/4) + %e;
O vetor [1 2 3] é armazenado na variável A e a expressão tan(%pi/4) + %e em s, porém nenhum resultado é mostrado na tela.
Um comando muito extenso pode ser continuado em uma próxima linha usando pontos suspensivos no final da linha:
s = 1 -1/2 + 1/3 -1/4 + 1/5 - 1/6 + 1/7 ...
- 1/8 + 1/9 - 1/10 + 1/11 - 1/12;
Qualquer coisa que apareça após de um par de barras // será ignorado, e serve para inserir comentários ou anotações:
%e^(%pi * %i) + 1 // deve ser igual a 0, usando a fórmula de Euler
ans =
Usando a seta vertical recuperamos os comandos digitados previamente.
Estrutura
de dados
Scilab suporta várias estruturas de dados. Como por exemplo: matrizes (reais ou complexas), polinômios, Booleanos, cadeia de caracteres, funções, listas, etc. Por favor, leia a documentação de Scilab com cuidado. Para inquirir sobre um objeto, digite:
typeof(objeto)
Cadeia
de caracteres
Para entrar uma cadeia de caracteres, feche-la entre aspas:
'Isto é uma cadeia de caracteres'
ou
"Isto é uma cadeia de caracteres"
Para concatenar caracteres use o operador + :
"Bem-vindo " + "ao " + "Scilab!"
ans =
Bem-vindo ao Scilab!
Salvando
e carregando variáveis
Para salvar e carregar variáveis usamos as funções save e load:
save('nome_ARQUIVO', var1, var2, ...);
load('nome_ARQUIVO', 'var1', 'var2', ...);
onde nome_ARQUIVO é o nome do arquivo a ser salvo ou carregado, e var1, var2,... são os nomes das variáveis.
a = 3; b = %f; s = 'scilab';
save('salve.dat', a, b, s);
clear a; // apaga a variável a
clear b;
clear s;
load('salve.dat', 'a', 'b', 's');
// carrega todas as variáveis salvas
load('salve.dat','b');
// carrega apenas a variável b
load('salve.dat','d');
// isto não gera mensagem de erro, a variável não está definida.
listvarinfile('salve.dat');
// lista as variáveis no arquivo
Name Type Size Bytes
----------------------------------------------------
a constant 1 by 1 24
b boolean 1 by 1 20
s string 1 by 1 44
 5. Com
Matrizes
5. Com
Matrizes
Editando
Matrizes
Existem diferentes formas de ingressar uma matriz.
1. Separe cada elemento da linha com um espaço em branco ou vírgula,
2. Separe cada coluna por um ponto e vírgula e
3. Coloque a lista completa dos elementos entre um par de colchetes.
Por exemplo, para entrar uma matriz 3 x 3 (o quadrado mágico) com o nome de variável M:
M = [8 1 6; 3 5 7; 4 9 2]
M =
8. 1. 6.
3. 5. 7.
4. 9. 2.
Calculando
somas
Para a matriz anterior gostaríamos conferir as somas dos elementos das linhas, colunas e da diagonal. Isto é feito com segue:
sum(M,'c') // soma coluna
ans =
15.
15.
15.
sum(M,'r') // soma linha
ans =
15. 15. 15.
A soma da diagonal é feita com a ajuda do comando diag.
D=diag(M);
sum(D,'r')
ans =
15.
Índices
É mais difícil achar a soma das outras diagonais. Um método é fazer a soma manualmente
M(1,3) + M(2,2) + M(3,1)
ans =
15.
Outra forma mais direta é usar a função mtlb_fliplr, onde mtlb é um comando do Matlab. O efeito que causa é rebater ou virar a matriz de esquerda para direita:
mtlb_fliplr(M)
ans =
6. 1. 8.
7. 5. 3.
2. 9. 4.
Agora o resultado desejado pode ser obtido digitando
sum(diag(mtlb_fliplr(M))).
O
operador colon : ( dois pontos)
O operador colon : é um dos mais importantes do Scilab. A expressão 1:10 resulta em uma matriz linha com elementos 1, 2, ..., 10, i.é.:
1:10
ans =
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
Para ter um espaçamento diferente devemos especificar o incremento:
10 : -2 : 2
ans =
10. 8. 6. 4. 2.
Expressões com índices e o operador: se referem a partes de uma matriz. M(i:j, k) mostra a i-éssima linha até a j-éssima linha da coluna k. Similarmente,
M(3,2:3)
ans =
9. 2.
Outros exemplos:
M(3,[3,2])
ans =
2. 9.
M([2,1], 3:-1:1)
ans =
7. 5. 3.
6. 1. 8.
O operador $, fornece o maior valor do índice é usado para determinar o último coeficiente de um vetor ou de uma matriz. Por exemplo, para acessar todos os elementos com exceção do último da última coluna digitamos:
M(1:$-1, $)
As vezes queremos uma única linha ou coluna completa. Para obter todos os elementos da segunda linha:
M(2,:)
ans =
3. 5. 7.
Geração
de matrizes simples
Algumas matrizes básicas podem ser geradas com um comando simples:
|
zeros
|
todos
zeros |
|
ones
|
todos
uns |
|
eye
|
matriz
identidade |
|
rand
|
elementos
aleatórios |
Alguns exemplos:
zeros(2,3)
ans =
0. 0. 0.
0. 0. 0.
8 * ones(2,2)
ans =
8. 8.
8. 8.
eye(2,3)
ans =
1. 0. 0.
0. 1. 0.
rand(1,3,'uniform') // mesmo que rand(1,3)
ans =
0.2113249 0.7560439 0.0002211
Concatenação
Concatenação é um processo que consiste em juntar pequenas partes de matrizes e uma única maior. Isto é feito colocando os elementos de matrizes em outra matriz:
a = [1 2 3]; b = [4 5 6]; c = [7 8 9];
d = [a b c]
d =
1. 2. 3. 4. 5. 6. 7. 8. 9.
e = [a; b; c]
e =
1. 2. 3.
4. 5. 6.
7. 8. 9.
A concatenação de linhas/colunas deve ser consistente:
x = [1 2]; y = [1 2 3];
z = [x; y]
!-error 6
inconsistent row/column dimensions
Também podemos concatenar matrizes blocos. Por exemplo:
[eye(2,2) 5*ones(2,3); zeros(1,3) rand(1,2)]
ans =
1. 0. 5. 5. 5.
0. 1. 5. 5. 5.
0. 0. 0. 0.6525135 0.3076091
Deletando
linhas e colunas
Um par de colchetes sem argumento representa uma matriz vazia. Isto pode ser usado para deletar as linhas ou as colunas de uma matriz. Para deletar a primeira e a terceira linha da matriz identidade procedemos como segue:
A = eye(4,4);
A([1 3],:) = []
A =
0. 1. 0. 0.
0. 0. 0. 1.
Se deletamos um único elemento de uma matriz temos como resultado um erro. Por exemplo:
A(1,2) = []
!-error 15
submatrix incorrectly defined
Se deletamos usando um único índice, o resultado poderia ser um vetor coluna:
B=[1 2 3; 4 5 6];
B(1:2:5)=[]
B =
4.
5.
6.
A
matriz inversa e a resolução de sistemas lineares
O comando inv(M) da a matriz inversa de M. Se a matriz for mal condicionada, aparecerá um aviso de alerta:
inv([1 2;2 4.0000001])
warning
matrix is close to singular or badly scaled. rcond = 2.7778D-09
ans =
40000001. - 20000000.
- 20000000. 10000000.
Resolver Ax = b, i.é., achar x que satisfaça a equação, onde A é uma matriz quadrada invertível e b é um vetor, é feito editando A\b :
A = rand(3,3), b = rand(3,1)
A =
0.2113249 0.3303271 0.8497452
0.7560439 0.6653811 0.6857310
0.0002211 0.6283918 0.8782165
b =
0.0683740
0.5608486
0.6623569
x = A \ b
x =
- 0.3561912
1.7908789
- 0.5271342
Outro método é digitar inv(A) * b. Embora produza o mesmo resultado é um processo mais devagar que A\b devido a que neste caso é utilizado o método de eliminação de Gauss que poupa esforço computacional.
Operações
com matrizes
Para somar 4 a cada coeficiente da matriz M podemos fazer M + 4 * ones(M) , melhor e mais fácil é M + 4.
Multiplicar por 2 a segunda coluna e por 3 a terceira de M pode ser feito usando o operador .* :
M .* [1:3; 1:3]
Outras operações são:
|
+
|
adição
|
|
-
|
subtração
|
|
.*
|
multiplicação
|
|
.^
|
potência
|
|
./
|
divisão
à direita |
|
.\
|
divisão
à esquerda |
Assim em vez de digitar
s = 1 -1/2 + 1/3 -1/4 + 1/5 - 1/6 + 1/7 ...
- 1/8 + 1/9 - 1/10 + 1/11 - 1/12;
podemos fazer
s = sum((1:2:12) .\ 1) - sum((2:2:12) .\ 1)
ou
s = sum(1 ./ (1:2:12)) - sum(1 ./ (2:2:12))
Observe que 1./1:2:12 é interpretado como (1.)/(1:2:12). Similarmente, 1:2:12.\1 é interpretado como 1:2:(12.)\1.
Para ingressar a matriz M = [1 2 3 4 5; 6 7 8 9 10], podemos usar:
M = zeros(2,5);
M(:) = 1:10;
Ainda podemos poupar esforço se usamos a função matriz, que re-dimensionaliza a matriz:
M = matrix(1:10,2,5)
Como podemos obter N = [1 2; 3 4; 5 6; 7 8; 9 10] usando um único comando?
O comando chamado size retorna a dimensão da matriz:
size(M)
ans =
2. 5.
entretanto size(M,1) retorna 2 (o número de linhas) e size(M,2) retorna 5 (o número de colunas).
 6. O
ambiente de programação
6. O
ambiente de programação
Criando
funções
Scilab possui um ambiente de programação que permite ao usuário criar suas próprias funções e livrarias. Isto pode ser feito usando o editor SciPad. Para invocar o editor, digite scipad() ou editor(), ou clique Editor na barra do menu.
Os arquivos tem extensão .sce e .sci. Para salvar um arquivo, clique em File e selecione Save. Para carregar um arquivo, selecione Load. Para executar um arquivo digite
exec('nome_arquivo_função');
na linha de comandos, ou clique no ícone Execute.
Para escrever uma função digite:
function [saida1, saida2, ...] = nome(ent1, ent2, ...)
onde function é o comando que indicar que está sendo definida uma função, saida1, saida2 e ent1, ent2, ..., são as variáveis de entrada e saída, respectivamente da função; as variáveis podem ser Booleanas, números, matrizes, etc., e nome é o nome da função. Inserimos a definição da função e no final digitamos o comando:
endfunction
para indicar a finalização da função.
As linhas com comentários começam com duas barras inclinadas //.
Exemplo:
function [d] = distance(x, y)
d=abs(x-y)
endfunction
// this function computes the distance
Uma função Scilab pode ser auto-chamada recursivamente.
Diferentemente de Matlab, Scilab permite declarações de funções múltiplas (com diferentes nomes de funções) dentro de um único arquivo.
Controle
de fluxo
As expressões lógicas estão dadas na tabela abaixo:
|
==
|
igual
|
|
~=
|
não
igual |
|
>=
|
maior
ou igual que |
|
<=
|
menor
ou igual que |
|
>
|
gmaior
que |
|
<
|
menor
que |
|
~
|
não
|
Se a expressão lógica for verdadeira, o valor da variável booleana será T (true: verdade), senão F (false).
O
comando if
Temos o bloco básico condicional a seguir:
if condição
bloco
end
O bloco será executado quando a condição for verdadeira. Os blocos aninhados if possuem a seguinte estrutura:
if condição_1
bloco_1
elseif condição_2
bloco_2
elseif condição_3
bloco_3
elseif ...
...
end
No seguinte exemplo podemos usar o fato de que uma função pode ser auto-chamada recursivamente para obter uma função que gera o n-éssimo termo da seqüência de Fibonacci:
function [K] = fibonacci(n)
//function [K] = fibonacci(n)
//Gera o n-éssimo termo da seqüência Fibonacci 0,1,1,2,3,5,8,13,...
if n==1
K = 0;
elseif n==2
K = 1;
elseif n>2 & int(n)==n // confere se n é um inteiro maior que 2
K = fibonacci(n-1) + fibonacci(n-2);
else
disp('erro! -- não é um interior positivo');
end
endfunction
Observamos que este não é um procedimento eficiente para gerar o n-éssimo termo quando n for grande.
O
laço for
Um laço de repetição básica tem a seguinte estrutura:
for variável = valor_inicial : passo : valor_final
bloco
end
O laço será executado um número fixo de vezes especificado. Uma versão levemente modificada é:
str = 'abcdr';
s = ''; // um carater vazio
for i = [1 2 5 1 3 1 4 1 2 5 1]
s = s + part(str, i);
end
disp(s);
s = abracadabra
O
comando while
Possui a seguinte estrutura:
while condição
bloco
end
O laço se repetirá até que a condição seja satisfeita. Veja o seguinte exemplo (Algoritmo Euclidiano).
function [n1] = hcf(n1, n2)
// n1 w n2 são inteiros positivos
if n2 > n1
tem = n2; n2 = n1; n1 = tem; // para garantir que n1>=n2
end
r = pmodulo(n1, n2); // resto quando n2 divide n1
n1 = n2; n2 = r;
while r ~= 0
r = pmodulo(n1, n2);
n1 = n2; n2 = r;
end
endfunction
Os
comandos break e continue
Existem duas formas de interromper um laço para depois começar com uma próxima iteração, respectivamente. Por exemplo:
// o usuário deve ingresar 10 números e os que forem
// inteiros devem ser acrescentados, o programa
// se deterá quando um número negativo seja ingressado.
resultado = 0;
for i = 1:10
tem = input('ingresse um número');
if tem < 0
break;
end
if tem ~= int(tem) // parte inteira
continue;
end
resultado = resultado + tem;
end
disp(resultado);
Programando
...
O conceito de vetores e matrizes booleanas é importante. A função find também é útil. Retrona os índices lógicos booleanos. Por exemplo:
M = [-1 2; 4 9]; M > 0
ans =
F T
T T
M(M > 0)'
ans =
4. 2. 9.
end
Por outra parte,
find(M > 0)
ans =
2. 3. 4.
M(find(M>0))'
ans =
4. 2. 9.
Observamos que M(M>0) da o resultado mais rápido que M(find(M>0). É importante diferenciar & e and, | e or. As primiras opções de cada par são operações por elementos entretanto as outras retornam valores de verdade obtidos sobre todos os coefecientes de uma matriz booleana.
M = [0 -2; 1 0]; M==0 | M==1
ans =
T F
T T
and(M >= 0) // verdade se e somente se todos os coeficientes são verdadeiros
ans =
F
or(M == -2) // falso se todas os coeficientes são falsos
ans =
T
Debugando
Uma das tarerfas mais tediosas em programação é debugar. Isto pode ser feito de duas formas: uma é usando o debugador do Scilab, ou modificando o programa como se indica a seguir:
Para inserir um ponto de parada usamos
pause
para terminar com pause usamos
abort
para ver a saida de uma função usamos
return
para mostrar as variáveis
disp (variable)
7.
Graficando
Gráficos
2D
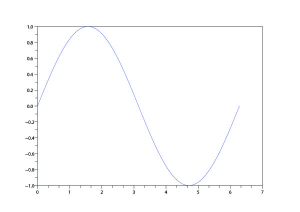
A função plot tem diferentes formas, dependendo do tipo dos argumentos de entrada. Se y for um vetor, plot(y) gera um gráfico linear por partes das componentes y versus o índice respectivo. No caso em que x e y sejam vetores da mesma dimensão, plot(x,y) gera um gráfico de y versus x. Por exemplo, para graficar o valor da função seno de zero a 2:
t = (0:1/100:2) * %pi;
|
|
Surferfícies
em 3D
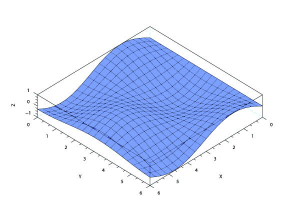
O comando plot3d(x,y,z) produz gráficos tridimensionais. Neste caso x e y são vetores linha cujas dimensões são n1 e n2, e z é uma matriz n1xn2 onde z(i,j) é o valor da altura da superfície no ponto (x(i),y(j)).
// gráfico elementar de z = f(x,y) |
|
 8. Scilab
versus Matlab
8. Scilab
versus Matlab
Scilab é um clone de Matlab ? Quase ...
· Matlab possui uma extensa e completa documentação; a de Scilab é resumida.
· Matlab possui um livrarias otimizadas e então é mais rápido que Scilab.
· Matlab possui uma ferramenta de computação muito poderosa chamado Simulink.
Scilab tem Scicos que tem os mesmos propósito porém é mais fraco.
· Matlab se integra muito melhor com outras linguagens de programação como C, C++ e Excel.
· As ferramenta gráficas de Scilab são comparativamente piores.
· Porém, o mais importante, Scilab é de graça. Devemos obervar que Scilab é recomendado para uso educacional.
 9.
Referências
9.
Referências
Em português1. Um curso de Scilab (Página do Prof. Paulo S. Motta Pires)
5.
Utilizando
o SCILAB na Resolução de Problemas
6.
Iniciação
ao Scilab (Prof. Luís Soares Barreto)
1.
A Preliminary Symbolic Toolbox for Scilab
Novembro 2008