Métodos de Euler e Runge-Kutta
Vamos descrever métodos numéricos para o problema de valor inicial (PVI):
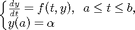
A ideia é particionar o intervalo [a,b] através de pontos igualmente espaçãdos:
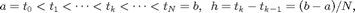
e construir construir aproximações para a solução $$y(t)$$ nesses pontos. Métodos que usam informação da solução no tempo anterior para construir a solução aproximada no tempo corrente são ditos métodos de passo simples ou métodos de um passo. No que segue vamos descrever o método de Euler e os métodos de Runge-Kutta de ordem 2, 3 e 4.
Contents
Método de Euler
As soluções aproximadas do método de Euler são definidas pela equação de diferençãs
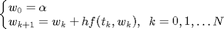
No MATLAB, o método de Euler pode ser implementado como segue:
% function y = euler(fun,alpha,a,b,N,grau) % % y = euler(fun,alpha,a,b,N,grau) % % METODO DE EULER: resolve um EDO de primeira ordem % com uma condicao inicial y(a)=alpha. % % DADOS: % fun - funcao continuamente diferenciavel % alpha - condicao inicial % [a,b] - intervalo % N - numero de passos % Default h=0.01 % grau - grau do metodo Euler, grau pode ser 1, 2 ou 3. % Default grau=1 % % Ismael Rodrigo Bleyer - 2006 h = abs(b-a)/N; k = 1; y = alpha; t = a; Y(k) = y; T(k) = t; switch grau case 1 for k = 2:(N+1) phi = feval(fun,t,y,0); t = t + h; T(k) = t; y = y + h*phi; Y(k) = y; end case 2 for k = 2:(N+1) phi = feval(fun,t,y,0) + (h/2)*[feval(fun,t,y,1)]; t = t + h; T(k) = t; y = y + h*phi; Y(k) = y; end case 3 for k = 2:(N+1) phi = feval(fun,t,y,0) + h/2*[feval(fun,t,y,1)] + (h^2)/6*[feval(fun,t,y,2)]; t = t + h; T(k) = t; y = y + h*phi; Y(k) = y; end otherwise error('Entrada incorreta: grau'); end
Error using ==> evalin Undefined function or variable 'b'.
Método Runge-Kutta
%function y = runge(fun,alpha,a,b,N,grau) % y = runge(fun,alpha,a,b,N,grau) % % METODO RUNGE-KUTTA encontra uma solucao numerica para uma EDO com uma % dada condicao inicial. % % DADOS: % fun - funcao string que define y'=f(t,y(t)) % alpha - condicao inicial y(a) = alpha % [a,b] - intervalo % N - numero de passos % grau - grau do metodo Runge-Kutta, grau pode ser 2, 3 ou 4. % Default grau=4. % % Ismael Rodrigo Bleyer - 2006 h = abs(b-a)/N; k = 1; y = alpha; t = a; Y(k) = y; T(k) = t; if nargin < 6, grau = 4; end switch grau case 2 for k = 2:(N+1) K1 = feval(fun,t,y); K2 = feval(fun,t+h,y+h*K1); y = y + h/2*[K1 + K2]; Y(k) = y; t = t + h; T(k) = t; end case 3 for k = 2:(N+1) K1 = feval(fun,t,y); K2 = feval(fun,t+(1/2)*h,y+(1/2)*h*K1); K3 = feval(fun,t+h,y+2*h*K2-h*K1); y = y + h/6*[K1 + 4*K2 + K3]; Y(k) = y; t = t + h; T(k) = t; end case 4 for k = 2:(N+1) K1 = feval(fun,t,y); K2 = feval(fun,t+(1/2)*h,y+(1/2)*h*K1); K3 = feval(fun,t+(1/2)*h,y+(1/2)*h*K2); K4 = feval(fun,t+h,y+h*K3); y = y + h/6*[K1 + 2*K2 + 2*K3 + K4]; Y(k) = y; t = t + h; T(k) = t; end otherwise error('grau nao confere') end
Exemplo Numérico
Ver arquivo pdf.