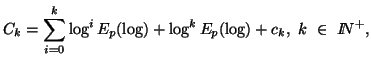This subsection deals with a measure of entropy commonly referred as entropy series, where in the probability distribution we have
This subsection deals with a measure of entropy commonly referred
as entropy series, where in the probability distribution we have ![]() .
This quantity is given by
.
This quantity is given by
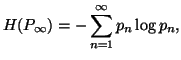
Let ![]() and
and ![]() be two sequences. Then it can easily be checked that the series
be two sequences. Then it can easily be checked that the series ![]() diverges and the series
diverges and the series![]() converges. Let
converges. Let![]() be the sum of the series. Consider
be the sum of the series. Consider ![]() ,
then
,
then
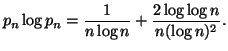
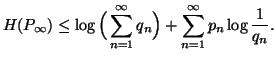
Property 1.64. If for some ![]() ,
then
,
then![]()
Property 1.65. For each nondecreasing probability sequence ![]() i.e.,
i.e., ![]() ,
the entropy series
,
the entropy series ![]() converges iff the series
converges iff the series
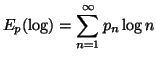
Property 1.66. For each nondecreasing sequence![]() ,
the following bound on the entropy series holds:
,
the following bound on the entropy series holds:
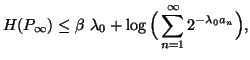
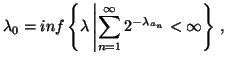
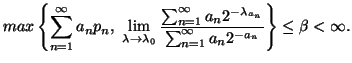
Property 1.67. For each nondecreasing probability sequence ![]() ,
the following bound on the entropy series hold:
,
the following bound on the entropy series hold:
Property 1.68. (Maximum-Entropy Principle). The entropy
series ![]() under the constraints
under the constraints
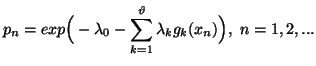
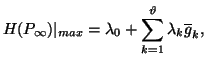
Note 1.6. Using the condition![]() ,
we get
,
we get
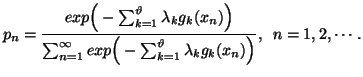 |
(1.12) |
By applying the conditions![]() ,
we can calculate the constants
,
we can calculate the constants![]() .
The probability distribution (1.12) is famous in the literature as ``Gibbs
distribution''.
.
The probability distribution (1.12) is famous in the literature as ``Gibbs
distribution''.
Particular cases: The property 1.69 admits the following interesting particular cases.
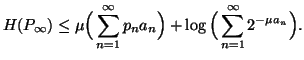
Property 1.70. The following bound on the entropy series holds:
The following properties are also worth emphasizing, whose details can be seen in Capocelli et al. (1988a;b)[25] [26].
Property 1.71. The following bound on the entropy series hold:
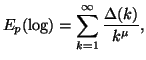
Property 1.72. The following bound on the entropy series hold:
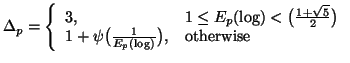
Property 1.73. For each nonincreasing probability distribution ![]() and for each
and for each ![]() ,
the following bound on the entropy series holds:
,
the following bound on the entropy series holds:
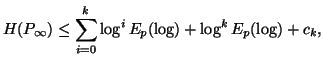
![$\displaystyle c_k=\log \Big[ \sum_{n=1}^{\infty}{exp_2\Big(-\big(\log^{k+1} n+\sum_{i=1}^{k+1}{\log^i n}\big)\Big)}\Big]+0.766k+0.531$](img404.gif)
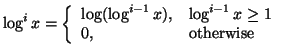
Property 1.74. For each nonincreasing probability distribution ![]() ,
the following bound on the entropy series holds:
,
the following bound on the entropy series holds:
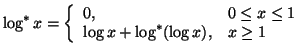
Property 1.75. For each nonincreasing probability distribution ![]() and for each
and for each ![]() ,
the following limits hold:
,
the following limits hold: