We see that the measure (2.1) is not symmetric in
We see that the measure (2.1) is not symmetric in![]() and
and ![]() . Its symmetric version known J-divergence (Jeffreys, 1946 [49]; Kullback and Leibler, 1961 [65]) is given by
. Its symmetric version known J-divergence (Jeffreys, 1946 [49]; Kullback and Leibler, 1961 [65]) is given by
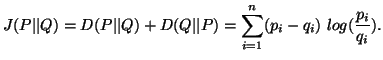
|
(2.7) |
Sibson (1969) [95] for the first time introduced the idea of information radius for a measure arising due to concavity property of Shannon's entropy. This measure recently referred as Jensen difference divergence measure is given by
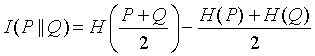
![$\displaystyle =\sum_{i=1}^n{\Big[{p_i\log p_i+q_i\log q_i\over2}-\Big({p_i+q_i\over 2}\Big) \log \Big({p_i+q_i\over2}\Big)\Big]}.$](img555.gif)
|
(2.8) |
By simple calculations, one can also write
![$\displaystyle I(P\vert\vert Q)= \frac{1}{2}\left[D\Big(P\vert\vert{P+Q\over2}\Big)+D\Big(Q\vert\vert{P+Q\over 2}\Big)\right].$](img556.gif)
|
(2.9) |
Taneja (1995) [108] studied an another kind of measure based on arithmetic and geometric mean inequality calling arithemetic and geometric mean divergence measure given by
![$\displaystyle T(P\vert\vert Q)= \frac{1}{2}\left[D\Big({P+Q\over2}\vert\vert P\Big)+D\Big({P+Q\over 2}\vert\vert Q\Big)\right]$](img557.gif)
|
|
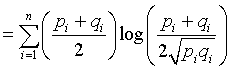
|
(2.10) |
Interestingly these three measures satisfy the following inequality:
![]()
The measures given by (2.7), (2.8) and (2.10) satisfy the following properties.
Property 2.17. We have
The measure ![]() used in the items (ii), (iii) and (v) is considered with natural logarithm
base.
used in the items (ii), (iii) and (v) is considered with natural logarithm
base.