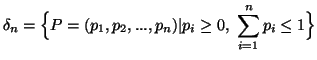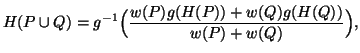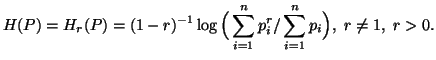Next:Entropy
of DegreeUp:Characterizations
of Generalized Entropies
Previous:Characterizations
of Generalized Entropies Go to:Table
of Contents
Entropy of Order r
The following characterization is due to Rényi (1961) [82].
Let us consider the following postulates defined for the function  ,
where
,
where
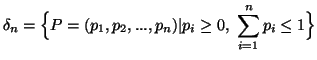
|
|
|
(3.15) |
-
(i) H(P) is a symmetric function of the elements of P.
-
(ii) If
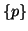 denotes the generalized probability distribution consisting of the single
probability
denotes the generalized probability distribution consisting of the single
probability 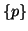 that
that 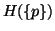 is a continuous function of p in the interval
is a continuous function of p in the interval 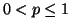 .
.
-
(iii)
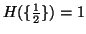 .
.
-
(iv) For
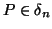 ,
, 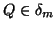 and
and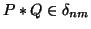 ,
we have
,
we have
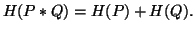
Before stating the last postulate, we introduce some notations. Let 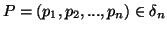 ,
and
,
and 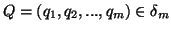 be two generalized probability distributions such that
be two generalized probability distributions such that 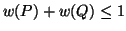 ,
we have
,
we have
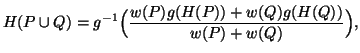 with
with 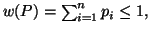 where
where 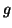 is strictly monotonic function.
is strictly monotonic function.
Then
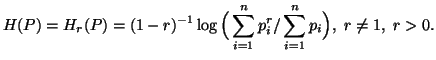 Later Daróczy (1963; 1964) [31], [32]
reformed the above axiomatic system. Based on the same motivations of Rényi,
later researchers (Aczél and Daróczy, 1963 [1];
Varma,1966 [119]; Kapur, 1967 [54]
and Rathie, 1970 [78]) generalized the entropy
of order
Later Daróczy (1963; 1964) [31], [32]
reformed the above axiomatic system. Based on the same motivations of Rényi,
later researchers (Aczél and Daróczy, 1963 [1];
Varma,1966 [119]; Kapur, 1967 [54]
and Rathie, 1970 [78]) generalized the entropy
of order 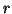 having more than one parameter. These generalizations are specified in
the list of entropies (see section 3.5.2).
having more than one parameter. These generalizations are specified in
the list of entropies (see section 3.5.2).
2001-06-21
![]() ,
where
,
where