Next:Generalized
Information and DivergenceUp:Important
Observations
Previous:List
of Generalized Entropies Go to:Table
of Contents
Generalized Distance Measures
The quantity 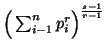 ,
, 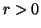 appearing in the unified expression (3.8) or in the entropy of order
appearing in the unified expression (3.8) or in the entropy of order 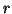 and degree
and degree 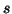 ,
i.e., in the expression (3.7) plays an important role. Let us write it
in the simplified form:
,
i.e., in the expression (3.7) plays an important role. Let us write it
in the simplified form:
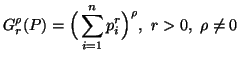
|
|
|
(3.22) |
for all 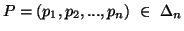 .
The quantity (3.49) is famous as generalized distance measure (Boekee
and Van der Lubbe, 1979 [15]; Capocelli et
al., 1985 [24]) or the generalized certainty
measure (Van der Lubbe et al., 1984 [116]).
.
The quantity (3.49) is famous as generalized distance measure (Boekee
and Van der Lubbe, 1979 [15]; Capocelli et
al., 1985 [24]) or the generalized certainty
measure (Van der Lubbe et al., 1984 [116]).
Another distance measure arising from the entropy of order 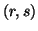 is given by
is given by
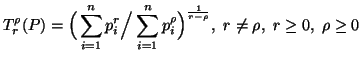
|
|
|
(3.23) |
for all 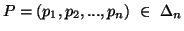 .
This measure has been considered by Capocelli et al. (1985) [24].
.
This measure has been considered by Capocelli et al. (1985) [24].
The quantities (3.49) and (3.50) contain as a particular case the measures
studied by Trouborst et al., (1974) [112],
Györfi and Nemetz (1975) [42], Devijver
(1974) [34], Vajda (1968) [113]
etc..
The measures (3.22) and (3.23) satisfy some properties. These are given
as follows:
Property 3.25. For all 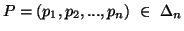 ,
we have
,
we have
-
(i)
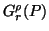 is a convex function of P for
is a convex function of P for 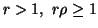 or
or 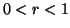 ,
,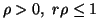 .
.
-
(ii)
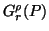 is a concave function of P for
is a concave function of P for 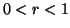 ,
,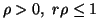 .
.
-
(iii)
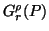 is a pseudoconvex/quasiconvex/Schur-convex function of P for
is a pseudoconvex/quasiconvex/Schur-convex function of P for 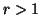 ,
, 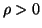 ,
or
,
or 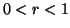 ,
, 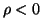 .
.
-
(iv)
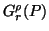 is a pseudoconcave/quasiconcave/Schur-concave function of P for
is a pseudoconcave/quasiconcave/Schur-concave function of P for 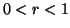 ,
, 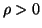 or
or 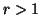 ,
, 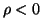 .
.
Property 3.26. For all 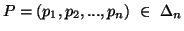 ,
we have
,
we have
-
(i)
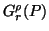 is a decreasing function of r (
is a decreasing function of r (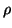 fixed and
fixed and 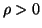 ).
).
-
(ii)
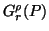 is an increasing function of r (
is an increasing function of r (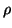 fixed and
fixed and 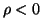 ).
).
-
(iii)
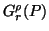 is a decreasing function of
is a decreasing function of 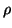 (r fixed and
(r fixed and 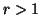 ).
).
-
(iv)
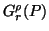 is an increasing function of
is an increasing function of 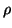 (r fixed and
(r fixed and 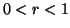 ).
).
Property 3.27. For all 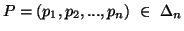 ,
,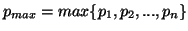 and
and 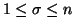 ,
we have
,
we have
-
(i) (
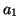 )
) 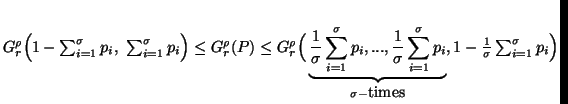
(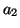 )
) 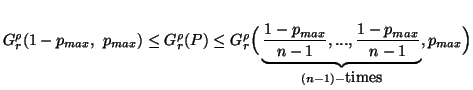
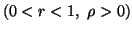 or
or 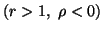 .
.
-
(ii) (
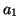 )
) 
( )
) 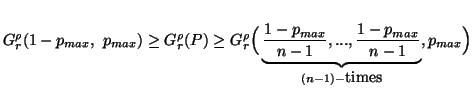
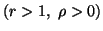 or
or 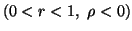 .
.
Property 3.28. For all 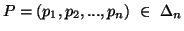 ,
we have
,
we have
-
(i)(
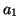 )
) 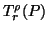 is an increasing function of r (
is an increasing function of r (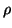 fixed).
fixed).
(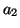 )
) 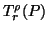 is an increasing function of
is an increasing function of 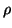 (r fixed).
(r fixed).
-
(ii) (
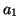 )
) 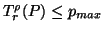 .
.
(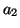 )
) 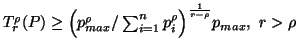 .
.
(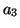 )
) 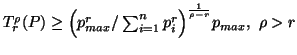 .
.
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
 ,
, 
![]() .
The quantity (3.49) is famous as generalized distance measure (Boekee
and Van der Lubbe, 1979 [15]; Capocelli et
al., 1985 [24]) or the generalized certainty
measure (Van der Lubbe et al., 1984 [116]).
.
The quantity (3.49) is famous as generalized distance measure (Boekee
and Van der Lubbe, 1979 [15]; Capocelli et
al., 1985 [24]) or the generalized certainty
measure (Van der Lubbe et al., 1984 [116]).
![]() is given by
is given by
![]() .
This measure has been considered by Capocelli et al. (1985) [24].
.
This measure has been considered by Capocelli et al. (1985) [24].
![]() ,
we have
,
we have
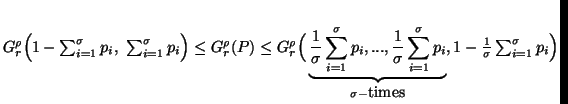
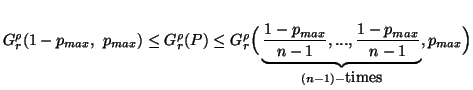
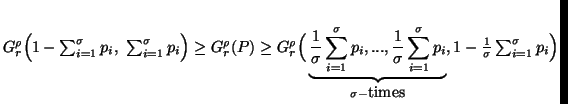
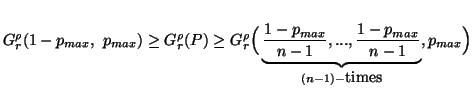
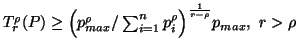 .
.
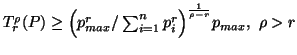 .
.