Let
Let ![]() be a discrete random variable taking a finite number of possible values
be a discrete random variable taking a finite number of possible values ![]() with probabilities
with probabilities ![]() respectively such that
respectively such that ![]()
![]() .
We attempt to arrive at a number that will measure the amount of uncertainty.
Let
.
We attempt to arrive at a number that will measure the amount of uncertainty.
Let ![]() be a function defined on the interval
be a function defined on the interval ![]() and
and ![]() be interpreted as the uncertainty associated with the event
be interpreted as the uncertainty associated with the event ![]() ,
,![]() or the information conveyed by revealing that
or the information conveyed by revealing that ![]() has taken on the value
has taken on the value ![]() in a given performance of the experiment. For each n, we shall define
a function
in a given performance of the experiment. For each n, we shall define
a function ![]() of the n variables
of the n variables ![]() .
The function
.
The function![]() is to be interpreted as the average uncertainty associated with the event
is to be interpreted as the average uncertainty associated with the event ![]() given by
given by
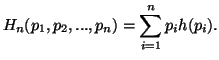 |
(1.1) |
Thus ![]() is the average uncertainty removed by revealing the value of
is the average uncertainty removed by revealing the value of ![]() .
For simplicity we shall denote
.
For simplicity we shall denote
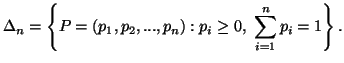
|
|
(1.2) |
for all ![]()
![]() and
and ![]()
![]() .
Replacing
.
Replacing ![]() by
by ![]()
![]() we get
we get
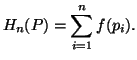 |
(1.3) |
Based on (1.2) and (1.3) we present the following theorem.
Theorem 1.1. Let ![]() be a function satisfying (1.2) and (1.3), where
be a function satisfying (1.2) and (1.3), where ![]() is real valued continuous function defined over [0,1]. Then
is real valued continuous function defined over [0,1]. Then ![]() is given by
is given by
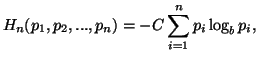 |
(1.4) |
where ![]() with
with ![]() .
.
The proof is based on the following Lemma (ref. Chaundy and McLeod, 1961 [27]).
Lemma 1.1. Let ![]() be a continuous function satisfying
be a continuous function satisfying
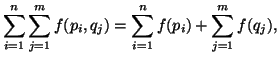 |
(1.5) |
for all ![]() Then
Then
|
|
(1.6) |
for all ![]() with
with ![]() .
.
Alternatively the measure (1.4) can be characterized as follows (ref. Shannon,1948 [86]; Feinstein, 1958 [36]).
Theorem 1.2. Let ![]() be a function satisfying the following axioms:
be a function satisfying the following axioms:
A third way to characterize the measure (1.4) is as follows (ref. Aczél and Daróczy, 1975 [2]).
Theorem 1.3. Let ![]() be a function satisfying the following axioms:
be a function satisfying the following axioms:
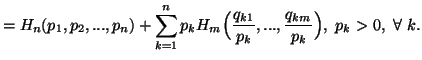
The following is a different way to characterize the measure (1.4). It is based on the functional equation famous as fundamental equation of information.
Theorem 1.4. Let ![]() be a function satisfying
be a function satisfying
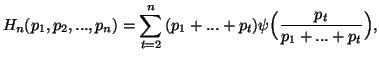
For simplicity, let us take ![]() in (1.4). If we put the restriction
in (1.4). If we put the restriction ![]() in the above theorems with
in the above theorems with ![]() ,
we get
,
we get ![]() .
This yields
.
This yields
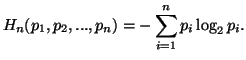 |
(1.7) |
For more characterizations of the measure (1.4) or (1.7) refer to Aczél
and Daróczy (1975) [2] and Mathai
and Rathie (1975) [71].