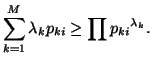Let
Let ![]() be
be![]() probability
distributions. Let
probability
distributions. Let ![]()
![]()
![]()
![]() .
It is well known that the Shannon's entropy satisfy the following
inequality:
.
It is well known that the Shannon's entropy satisfy the following
inequality:
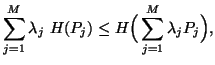 |
(5.1) |
with equality iff ![]() .
.
Also due to property 1.14, we have
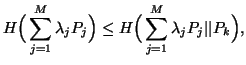 |
(5.2) |
for each k=1,2,...,M with equality iff ![]() .
.
We can easily check that
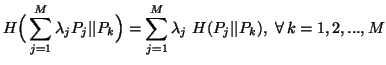 |
(5.3) |
Multiplying both sides of (5.2) by ![]() ,
summing over k=1,2,...,M and using (5.3), we have
,
summing over k=1,2,...,M and using (5.3), we have
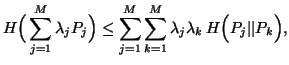 |
(5.4) |
with equality iff ![]() .
.
From (5.1) and (5.4), we have
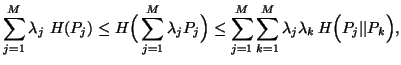 |
(5.5) |
with equality iff ![]() .
.
The above inequality (5.5) admits the following three nonnegative differences given by
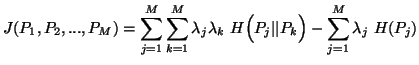
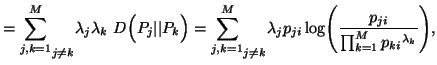 |
(5.6) |
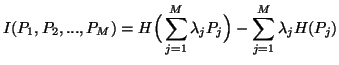
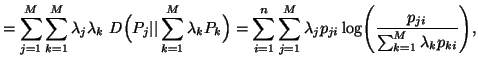 |
(5.7) |
and
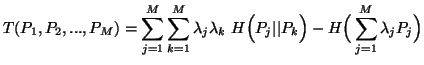
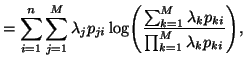 |
(5.8) |
From (5.6), (5.7) and (5.8), we conclude that
|
|
(5.9) |
From (5.9), we have the following inequalities:
|
|
(5.10) |
and
|
|
(5.11) |
The measures (5.6), (5.7) and (5.8) in particular reduce to (2.6) and
(2.7) respectively, when M=2, ![]() and
and![]() with a multiplicative constant.
with a multiplicative constant.
Note 5.1.