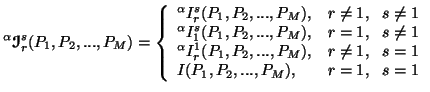 |
(5.12) |
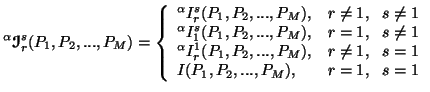 |
(5.12) |
![]() and 3, where for
and 3, where for ![]() ,
we have
,
we have
![$\displaystyle ^1I^s_r(P_1,P_2,...,P_M)= (1-2^{1-s})^{-1} \Big\{ \Big[\sum_{......lambda_k p_{ki}}\Big)^{1-r}}\Big]^{s-1\over r-1} -1\Big\},\ r\neq 1,\ s\neq 1$](img1143.gif)
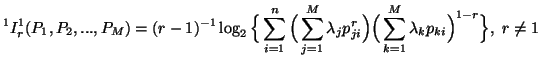
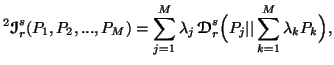 |
(5.13) |
For ![]() we have
we have
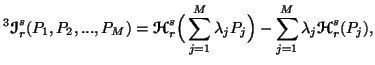 |
(5.14) |
where ![]() and
and ![]() are as given in chapter 3 and chapter 4 by expressions (3.8) and (4.1)
respectively.
are as given in chapter 3 and chapter 4 by expressions (3.8) and (4.1)
respectively.
In particular we have
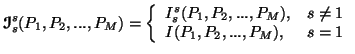
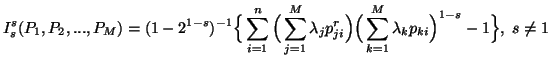
For two-dimensional case, i.e., when M=2, ![]() ,
, ![]() and
and![]() ,
we have
,
we have
![]()
![$\displaystyle = (1-2^{1-s})^{-1}\Big\{ \Big[ \sum_{i=1}^n{ \Big({p^r_i+q^r_i\over 2}\Big)\Big({p_i +q_i\over2}\Big)^{1-r}}\Big]^{s-1\over r-1}-1\Big\},$](img1156.gif) |
(5.15) |
![]()
![$\displaystyle = (1-2^{1-s})^{-1}\, {1\over 2} \Big\{ \Big[ \sum_{i=1}^n{p^r_i\......um_{i=1}^n{q^r_i\Big({p_i +q_i\over2}\Big)^{1-r}}\Big]^{s-1\over r-1}-2\Big\},$](img1158.gif) |
(5.16) |
![]()
![$\displaystyle = (1-2^{1-s})^{-1}\Big\{ {1\over 2} \Big[ \Big( \sum_{i=1}^n{p^r......g] -\Big[\sum_{i=1}^n{\Big({p_i+q_i\over 2}\Big)^r}\Big]^{s-1\over r-1}\Big\},$](img1160.gif) |
(5.17) |
for all ![]() .
.
Note 5.2.The measures (5.15) and (5.16) are the same as given
in (4.10) and (4.6) respectively. While the measure (5.17).