Next:Entropy
of Degree andUp:Properties
of Unified Conditional
Previous:Multivariate
Cases Go to:Table
of Contents
Unified (r,s)-Mutual
Information
In this section, we present six different ways to define the unified 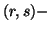 mutual
information.
mutual
information.
Let us consider
 and and
|
|
|
(6.6) |
and
 and and
|
|
|
(6.7) |
where

|
|
|
(6.8) |
and
 etc.
etc.
We call the measures  (
(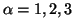 and
and  )
the unified
)
the unified 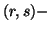 mutual
information among the random variables
mutual
information among the random variables 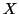 and
and 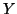 .
The measures
.
The measures  (
(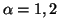 and
and 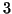 )
we call the unified
)
we call the unified 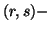 mutual
information among the random variables
mutual
information among the random variables 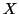 and
and 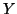 given
given 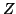 .
.
Property 6.14. We have
-
(i)
 (resp.
(resp.  )
(
)
(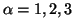 and
and 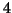 ),
with equality iff
),
with equality iff 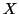 and
and 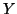 are independent.
are independent.
-
(ii)
 (resp.
(resp.  )
(
)
(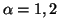 and
and 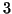 ),
with equality iff
),
with equality iff 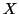 and
and 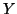 are independent given
are independent given 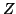 .
.
The above property 6.12 holds under the following conditions:
-
(
 )
For
)
For 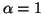 ,
, 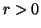 with
with 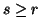 or
or 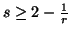 (resp.
(resp. 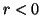 with
with or
or  );
);
-
(
 )
For
)
For 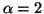 and 3,
and 3,  (resp.
(resp. 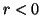
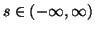 );
);
-
(
 )
For
)
For 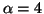 ,
,  (resp.
(resp. 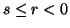 )
(only for part(i)).
)
(only for part(i)).
Note 6.4. Similar to Shannon's entropy (property 1.51) we left
for the readers to check the validity of the following inequality:
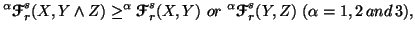
i.e., to find the conditions on the parameters 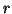 and
and 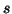 for the validity of the above expression.
for the validity of the above expression.
Property 6.15. We have
 and and
|
|
|
(6.9) |
Note 6.5. The relation (6.9) is famous as
"additive property".
It also hold when 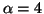 ,
but at moment, we are not aware of the conditons on
,
but at moment, we are not aware of the conditons on 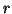 and
and 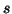 for which
for which is nonnegative, but the particular case when
is nonnegative, but the particular case when  is discussed in section 6.4
is discussed in section 6.4
For Simplicity, let us write
 and
and forall
forall  .
.
We have


where 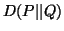 is as given in (2.1)
is as given in (2.1)
We can write
 where
where
 for all
for all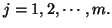
Thus
 The two more ways to define the unified
The two more ways to define the unified 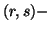 mutual
information are given by
mutual
information are given by

|
|
|
(6.10) |

|
|
|
(6.11) |
where  is as given by (4.1).
is as given by (4.1).
Property 6.16. For  and
and 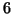 ,
we have
,
we have
-
(i)
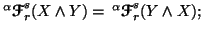
-
(ii)
 with equality iff
with equality iff 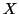 and
and 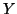 are independent.
are independent.
-
(iii)
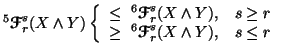
Note 6.6. If we consider the fifth and sixth way of unified 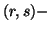 conditional
entropies in the following way
conditional
entropies in the following way

|
|
|
(6.12) |
then, we don't know for what values of 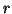 and
and 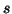 the measures given in (6.12) turn out to be nonnegative.
the measures given in (6.12) turn out to be nonnegative.
Note 6.7. Some of the above generalized mutual information
measures can be connected to unified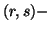 divergence
measures given in Chapter 5. These connections are as follows:
divergence
measures given in Chapter 5. These connections are as follows:
In (5.12), take  and
and  ,
we get
,
we get
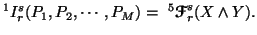
Similarly, we can write
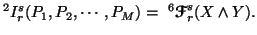

In the notes 6.4 and 6.5, we have seen that there are difficulties in
getting certain values of 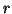 and
and 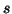 for which the measures
for which the measures or
or  and
and 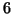 )
become nonnegative. But, in the particular case, when
)
become nonnegative. But, in the particular case, when  ,
the above difficulties are overcomed. The particular case for
,
the above difficulties are overcomed. The particular case for 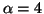 is discussed in the following subsection.
is discussed in the following subsection.
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil

![]() (
(![]() and
and ![]() )
the unified
)
the unified ![]() mutual
information among the random variables
mutual
information among the random variables ![]() and
and ![]() .
The measures
.
The measures ![]() (
(![]() and
and ![]() )
we call the unified
)
we call the unified ![]() mutual
information among the random variables
mutual
information among the random variables ![]() and
and ![]() given
given ![]() .
.
![]()
![]() and
and ![]() for the validity of the above expression.
for the validity of the above expression.

![]() is as given in (2.1)
is as given in (2.1)




![]() and
and ![]() ,
we have
,
we have
 with equality iff
with equality iff 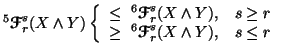
![]() divergence
measures given in Chapter 5. These connections are as follows:
divergence
measures given in Chapter 5. These connections are as follows:
![]() and
and ![]() ,
we get
,
we get
![]()
![]()
![]() and
and ![]() for which the measures
for which the measures![]() or
or ![]() and
and ![]() )
become nonnegative. But, in the particular case, when
)
become nonnegative. But, in the particular case, when ![]() ,
the above difficulties are overcomed. The particular case for
,
the above difficulties are overcomed. The particular case for ![]() is discussed in the following subsection.
is discussed in the following subsection.