Next:Mutual
Information of DegreeUp:Entropy
of Degree and
Previous:Entropy
of Degree and Go to:Table
of Contents
Conditional Entropies of Degree
s
Based on the above definition of entropy of degree 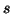 the different ways of conditional entropies of degree
the different ways of conditional entropies of degree 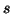 are as follows:
are as follows:
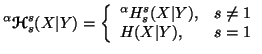
for 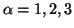 and
and 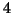 ,
where
,
where
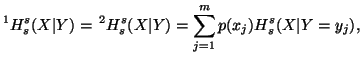
![$\displaystyle ^3H^s_s(X\vert Y) = (2^{1-s}-1)^{-1} \left\{\left[\sum_{j=1}^m\......\sum_{i=1}^n p(x_i\vert y_j)^s\right)^{1/s}\right]^s -1\right\},\,\,s \neq 1 $](img1375.gif) and
and
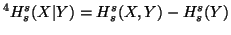 with
with
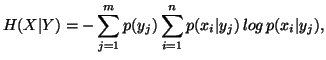 and
and
![$\displaystyle H^s_s(X\vert Y=y_j) = (2^{1-s}-1)^{-1}\big[\sum_{i=1}^n p(x_i\vert y_j)^s -1\big], \,\, s \neq 1,$](img1378.gif) for all
for all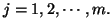
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
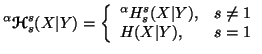
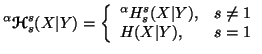
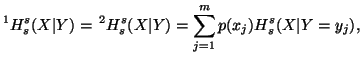
![$\displaystyle ^3H^s_s(X\vert Y) = (2^{1-s}-1)^{-1} \left\{\left[\sum_{j=1}^m\......\sum_{i=1}^n p(x_i\vert y_j)^s\right)^{1/s}\right]^s -1\right\},\,\,s \neq 1 $](img1375.gif)
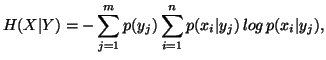
![$\displaystyle H^s_s(X\vert Y=y_j) = (2^{1-s}-1)^{-1}\big[\sum_{i=1}^n p(x_i\vert y_j)^s -1\big], \,\, s \neq 1,$](img1378.gif)