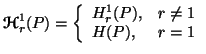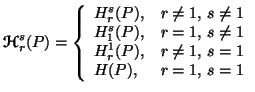 |
(3.8) |
Instead of studying the properties of the entropies (3.1), (3.3),
(3.5), (3.6) and (3.7) separately, our aim here is to study them in a unified
way. This unification is as follows:
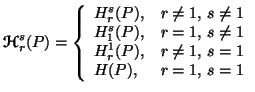 |
(3.8) |
for all ![]() and
and ![]() ,
where
,
where![]() is the same as
is the same as ![]() given in (3.1). From now onwards, we shall use the notation
given in (3.1). From now onwards, we shall use the notation ![]() instead of
instead of ![]() .
.
The entropies ![]() and
and ![]() do not appear in the unified expression (3.8) because they are particular
cases of
do not appear in the unified expression (3.8) because they are particular
cases of![]() ,
and hence are already contained in it. According to the notations above,
,
and hence are already contained in it. According to the notations above, ![]() given in (3.3) means
given in (3.3) means ![]() for
for![]() in
in ![]() .
Henceforth, we shall consider this notation too.
.
Henceforth, we shall consider this notation too.
It is customary to study the generalized measure given in (3.8) for
positive values of ![]() and
and ![]() .
Taneja (1989) [105] and Taneja et al. (1989)
[109] studied then for
.
Taneja (1989) [105] and Taneja et al. (1989)
[109] studied then for ![]() and any
and any ![]() .
The natural question arises, why to keep
.
The natural question arises, why to keep![]() ?
Why not to study them for
?
Why not to study them for ![]() .
This is our aim in this chapter i.e., to study the measure (3.8) for
.
This is our aim in this chapter i.e., to study the measure (3.8) for ![]() .
By considering
.
By considering ![]() ,
again the problem arises is that, we can find probability distributions
such that the measure (3.8) become infinite. To avoid this, we shall redefine
the set
,
again the problem arises is that, we can find probability distributions
such that the measure (3.8) become infinite. To avoid this, we shall redefine
the set ![]() in the following way:
in the following way:
 with
withWe call, the unified expression (3.8), i.e.,![]() ,
the unified
,
the unified ![]() entropy.
entropy.
From the unified expression (3.8), we observe that![]() is a continuous extension of
is a continuous extension of ![]() with respect to the parameters. In order to study the properties of
with respect to the parameters. In order to study the properties of ![]() it is sufficient to study the properties of
it is sufficient to study the properties of ![]() for
for ![]() ,
because the rest part follows by continuity with respect to
,
because the rest part follows by continuity with respect to ![]() and
and ![]() .
For simplicity, this observation is denoted as follows:
.
For simplicity, this observation is denoted as follows:
|
|
(3.9) |
where "CE" means "continuous extension" with respect to the parameters ![]() and
and ![]() .
.
Note 3.1. The notations ![]() and
and ![]() are understood as follows:
are understood as follows: