Property 3.1. (Continuity).![]() is a continuous function of P.
is a continuous function of P.
Property 3.2. (Symmetry).![]() is a symmetric function of its arguments i.e.,
is a symmetric function of its arguments i.e.,
Property 3.3. (Normality). We have
![]()
![$\displaystyle {\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)=g^{-1}\bigg[......{p_ig\big({\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r\{p_i\}\big)}\bigg],$](img683.gif)
![$\displaystyle {\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(\{p_i\})=\left\......2^{1-s}-1)\big[p^{s-1}_i -1\big], & s\neq 1 \\ -\log p_i\end{array}\right.$](img684.gif)
Property 3.6. (Nonnegativity).![]() with equality iff
with equality iff ![]() ,
where
,
where![]() is a probability distribution such that one of the probabilities is one
and all others are zero i.e.,
is a probability distribution such that one of the probabilities is one
and all others are zero i.e.,![]() .
.
Property 3.7. (Monotonicity).![]() is a monotonic decreasing function of
is a monotonic decreasing function of ![]() (
(![]() fixed).
fixed).
Property 3.8. (Inequalities among generalized entropies). The following inequalities hold
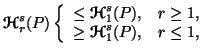
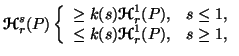
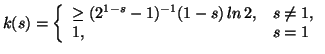

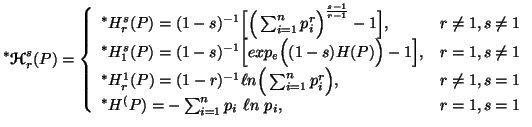 |
(3.12) |
where "![]() "
represents the logarithms with natural base "e".
"
represents the logarithms with natural base "e".
Based on the expression (3.15), the properties 3.7 and 3.8 are extended as follows:
Property 3.7*.![]() is also a decreasing function of
is also a decreasing function of ![]() (
(![]() fixed). In particular, when
fixed). In particular, when![]() ,
the result still holds.
,
the result still holds.
Property 3.8*. Parts (ii) and (iii) of the property 3.8 are simplified as follows:
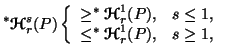

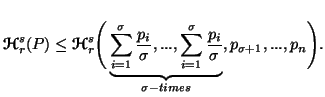
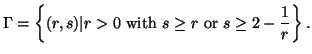 |
(3.13) |
Note 3.3. The condition ![]() is better than
is better than ![]() ,
, ![]() ,
but it holds for
,
but it holds for ![]() .
For
.
For ![]() ,
we need
,
we need ![]() .
In particular, when
.
In particular, when ![]() ,
the condition
,
the condition ![]() does not work. In this case, we need the second condition, i.e.,
does not work. In this case, we need the second condition, i.e., ![]() ,
, ![]() .
In particular, when
.
In particular, when ![]() ,
, ![]() or
or ![]() both the conditions, i.e.,
both the conditions, i.e., ![]() or
or ![]() ,
, ![]() works well.
works well.
Property 3.11. (Concavity for n=2). For![]() ,
, ![]() is concave for all
is concave for all![]() .
.
Property 3.12. (Schur-concavity).![]() is a Schur-concave of
is a Schur-concave of ![]() .
.
Property 3.13. (Maximality).![]() is maximum for the uniform probability distribution i.e.,
is maximum for the uniform probability distribution i.e.,
Property 3.15. (Quasiconcavity).![]() is a quasiconcave function of P in
is a quasiconcave function of P in![]() .
.
Property 3.16. (Relative to maximum probability). Let ![]() ,
where
,
where![]() ,
then the followings hold:
,
then the followings hold:
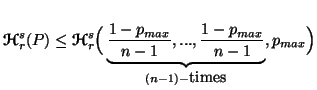 .
.![$ \lim_{r\to \infty}{ {\bf {\ensuremath{\boldsymbol{\mathscr{H}}}}}^s_r(P)}=\l......p^{s-1}_{max}-1],\\ s\neq 1 \\ -\log\, p_{max},\ \ s=1\end{array}\right.$](img717.gif)