Next:Multivariate
CasesUp:Properties
of Unified Conditional
Previous:Properties
of Unified Conditional Go to:Table
of Contents
Bivariate Cases
In this subsection, we shall give properties of the generalized
conditional entropies for the bivariate case.
Property 6.1. For 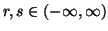 ,
we have
,
we have
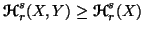 or
or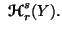
Property 6.2. We have
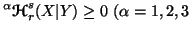 and
and
Property 6.3. If  and
and  are independent random variables, then
are independent random variables, then

Property 6.4. For any  and
and  ,
we have
,
we have
![$\displaystyle =(2^{1-s}-1)^{-1}\{\exp_2[(1-s)({\ensuremath{\boldsymbol{\mathscr{H}}}}^1_r(Y)+{\ensuremath{\boldsymbol{\mathscr{H}}}}^1_r(X\vert Y))]-1\}.$](img1285.gif)
Property 6.5. The following inequalities hold:
-
(i)
-
(ii)
-
(iii)

-
(iv)
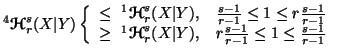
Note 6.2. The conditions 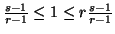 are equivalent to either
are equivalent to either 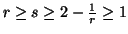 or
or  ,
,  ,
and the conditions
,
and the conditions  are equivalent to either
are equivalent to either  ,
,  or
or 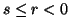 .
.
Property 6.6. We have
-
(i)
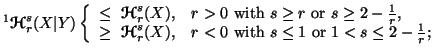
-
(ii)
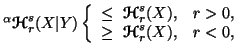 for
for  =2
and 3;
=2
and 3;
-
(iii)
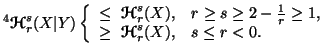
The equality sign holds iff  and
and  are independent random variables.
are independent random variables.
As a consequence of properties 6.5 and 6.6, we have the following property:
Property 6.7. (i) For 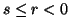 ,
we have
,
we have
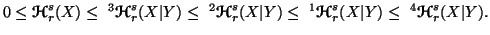
(ii) For  ,
we have
,
we have

(iii) For 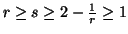 ,
we have
,
we have
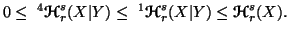
(iv) For 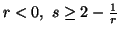 ,
we have
,
we have
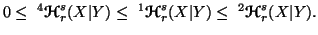
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
![]() ,
we have
,
we have
![]() or
or![]()
![]() and
and ![]() are independent random variables, then
are independent random variables, then
![]()
![]()
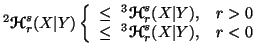
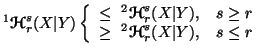

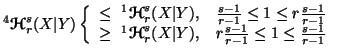
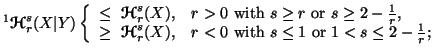
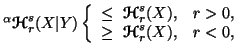 for
for 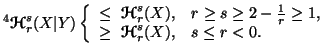
![]() ,
we have
,
we have
![]()
![]()
![]()
![]()