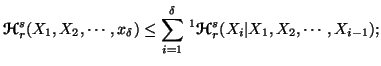Next:Unified
Mutual InformationUp:Properties
of Unified Conditional
Previous:Biveriate
Cases Go to:Table
of Contents
Multivariate Cases
In this subsection, we shall extend the results studied in Section
6.2.1 for three or more random variables. These are given by the following
properties:
Property 6.8. We have
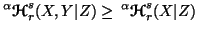 or
or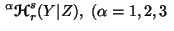 and
and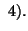
Property 6.9. We have
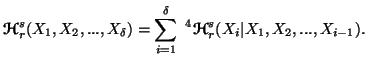 Property 6.10. We have
Property 6.10. We have
-
(i)
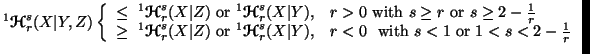
-
(ii)
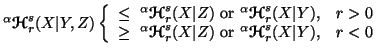 for
for  =2
and 3;
=2
and 3;
The equality sign holds in (i) and (ii) iff  and
and  are independent given Z, i.e., iff
are independent given Z, i.e., iff 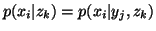 or
or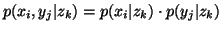 ,
,  i,j,k.
i,j,k.
Property 6.11. We have
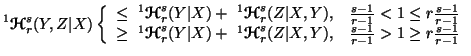
Property 6.12. For all 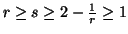 ,
we have
,
we have
-
(i)
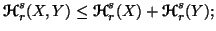
-
(ii)
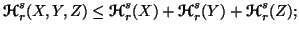
-
(iii)
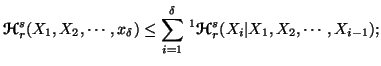
-
(iv)
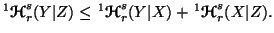
Property 6.13. If
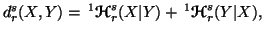 then for all
then for all 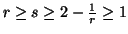 ,
we have
,
we have
-
(i)
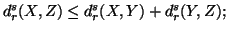
-
(ii)
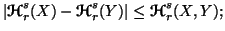
-
(iii)
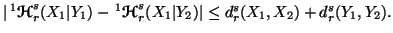
Note 6.3. It is interesting to verify the properties 6.11, 6.12
and 6.13 for the measures 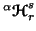 (
( and
and  )
and
to find the conditions of their validites.
)
and
to find the conditions of their validites.
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
![]() or
or![]() and
and![]()
![]() or
or![]() and
and![]()
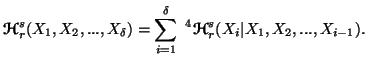
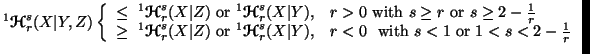
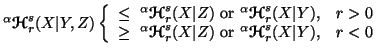 for
for 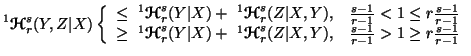
![]() ,
we have
,
we have