


Next: Propriedades da medida de
Up: Medida de Lebesgue em
Previous: Introdução
Medida de Lebesgue
Definição 1.2.1
Um intervalo em
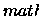
é um conjunto da forma
[a,b], (a,b], (a,b), [a,b) com
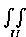
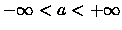
ou
da
forma
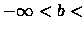
![$[a,+\infty),\ \ (-\infty, b],\ \ (-\infty, b)$](img10.gif)
with

or finally
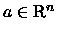
.
Denotaremos um tal intervalo por J. Por |J| queremos denotar o
comprimento de J.
Definição 1.2.2
Um retângulo em R
n
é um conjunto da forma
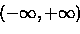 |
(1.1) |
onde os
Ji são intervalos.
O volume de Q, vol(Q), define-se como:
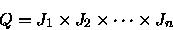 |
(1.2) |
Definição 1.2.3
A medida exterior ( ou medida exterior de Lebesgue)
de um conjunto
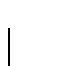
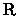
define-se como:
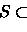 |
(1.3) |
onde o ínfimo é tomado sobre todas as famílias finitas ou
enumeráveis
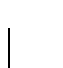
de retângulos tais que
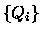
.
De (a), (b) e (c) decorre o seguinte Corolário que melhora a
propriedade (c):
Uma função
 onde
onde
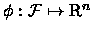 é aditiva se vale
é aditiva se vale
sempre que
 .
Decorre do corolário que m* é aditiva
sobre pares de conjuntos disjuntos se um deles é aberto ou fechado. Daremos
agora um exemplo de conjuntos disjuntos para os quais não vale a aditividade
da medida exterior de Lebesgue:
.
Decorre do corolário que m* é aditiva
sobre pares de conjuntos disjuntos se um deles é aberto ou fechado. Daremos
agora um exemplo de conjuntos disjuntos para os quais não vale a aditividade
da medida exterior de Lebesgue:
Exemplo 1.1
Seja
![$T:[0,1]\to [0,1]$](img29.gif)
definida por
onde

.
Observe que
T é uma bijeção . Uma órbita de
T é um conjunto da
forma
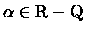
onde
![$x\in [0,1]$](img33.gif)
.
Duas órbitas são
disjuntas ou coincidem. O conjunto das órbitas forma, pois uma partição
de [0,1]. Seja
A0 o conjunto obtido pela escolha de um ponto em cada
órbita de
T. Observe que estamos usando aqui o axioma da escolha. De fato
este exemplo não pode ser construido sem o axioma da escolha.
Afirmação 1. Se 
 .
.
Prova: Se
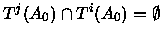 então
x=Tj(y)=Ti(z) with
então
x=Tj(y)=Ti(z) with
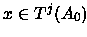 .
Mas então
y=T-j(x) and
z=T-i(x). Suponhamos sem perda de generalidade que x>y. Então
existe
.
Mas então
y=T-j(x) and
z=T-i(x). Suponhamos sem perda de generalidade que x>y. Então
existe
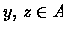 tal que i=j+k. Segue que
tal que i=j+k. Segue que
Tk(z)=Tk(T-j-k(x))=T-j(x)=y
isto é y pertence à órbita de z e 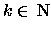 ,
o que é uma
contradição.
,
o que é uma
contradição.
Afirmação 2.
![$[0,1]=\bigcup\limits_{j=-\infty}^{\infty}
T^j(A_0).$](img40.gif)
Seja
![$x\in [0,1]$](img33.gif) .
Então, x pertence a alguma órbita de T.
Seja
.
Então, x pertence a alguma órbita de T.
Seja
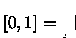 o elemento de A) nesta órbita. Então existe
o elemento de A) nesta órbita. Então existe
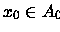 tal que
x=Tk(x0), isto é
tal que
x=Tk(x0), isto é
Afirmação 3.

Isto segue de que m* pode ser definida usando-se apenas
intervalos que não contém o ponto 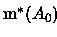 .
E para estes intervalos vale
que
.
E para estes intervalos vale
que
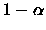 .
.
Se
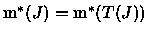 fosse válida para quaisquer
fosse válida para quaisquer
![$A,\;B\subset\, [0,1]$](img48.gif) disjuntos, então fazendo
Aj=Tj(A0) teríamos
disjuntos, então fazendo
Aj=Tj(A0) teríamos
Segue que
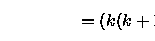 ,
isto é ,
,
isto é ,
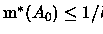 .
Mas, neste caso,
.
Mas, neste caso,
Deste modo vê-se que a medida exterior não é aditiva em
 .
O objetivo natural seria encontrar
uma família de subconjuntos de
.
O objetivo natural seria encontrar
uma família de subconjuntos de
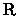 que contivesse os abertos e fechados (isto é a topologia) e
para a qual
que contivesse os abertos e fechados (isto é a topologia) e
para a qual
 fosse aditiva. Além disto é também razoável procurar
uma tal
família de modo a ser fechada por uniões e interseções
enumeráveis. Antes de passarmos a estudar este problema provemos o
teorema 1.2.1
fosse aditiva. Além disto é também razoável procurar
uma tal
família de modo a ser fechada por uniões e interseções
enumeráveis. Antes de passarmos a estudar este problema provemos o
teorema 1.2.1
Na prova do teorema 1.2.1 usaremos o seguinte lema:
Lema 1.2.1
.
Para todo
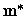
e

vale:
onde

indica o ínfimo das somas a direita tomadas
sobre todos os recobrimentos {
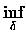
} de
E por
famílias de
retângulos com
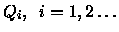
para todo
i.
![\begin{proof}% latex2html id marker 240
[Prova.] Para provar este lema come\c ca...
...\le
\inf \:\mathop{\pmb{\sum}} _i \mbox{vol}( Q_i)
\end{displaymath}\end{proof}](img65.gif)
![\begin{proof}% latex2html id marker 296
[Prova do teorema~\ref{T:med.bpem}.]
(a...
...l}(Q_i)
\end{displaymath}\noindent como quer\'\i amos demonstrar.\\
\end{proof}](img66.gif)
![\begin{proof}% latex2html id marker 382
[Prova do Corol\'ario~\ref{C:med.tecn}]....
...\infty A_n$\space \ e usando a defini\c c\~ao dos $A_n$ 's
temos que
\end{proof}](img67.gif)
Provados o teorema 1.2.1 e o corolário 1.2.1
continuamos na nossa busca de uma
família de subconjuntos de
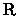 para a qual a medida
exterior seja aditiva.
Para tal introduzimos as seguintes definições estabelecidas essencialmente
por Caratheodory.
para a qual a medida
exterior seja aditiva.
Para tal introduzimos as seguintes definições estabelecidas essencialmente
por Caratheodory.
Definição 1.2.4
Dizemos que

separa o par
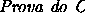
se

e
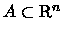
.
Definição 1.2.5
Dizemos que
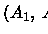
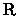
é mensurável se
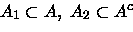 |
(1.4) |
para todo par (
A1,
A2) separado por
A.
Teorema 1.2.2
(a). Todo fechado ou aberto é mensurável.
(b). A diferença de conjuntos mensuráveis é
mensurável.
(c). As uniões enumeráveis de mensuráveis são
mensurá-
veis.
A família de conjuntos mensuráveis denota-se
 e se,
e se,
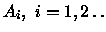 ,
sua medida
exterior de Lebesgue denota-se m(A) e se
denomina medida de Lebesgue de A. A família
,
sua medida
exterior de Lebesgue denota-se m(A) e se
denomina medida de Lebesgue de A. A família
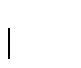 e a função
e a função
![$m:\boldsymbol{ \boldsymbol{ \mathscr{M} } }(\mathbb{R} ^n)\to [0,+\infty]$](img78.gif) são casos particulares do
contexto mais geral dado pelas seguintes definições:
são casos particulares do
contexto mais geral dado pelas seguintes definições:
Definição 1.2.6
Seja
X um conjunto. Uma família

de
subconjuntos de
X é
uma
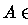
-álgebra se satisfaz:
- 1.
-
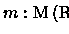 .
.
- 2.
-
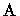 .
.
- 3.
-
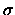 .
.
Usando um raciocínio elementar podemos a partir destas propriedades
obter as seguintes:
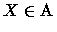 e que
e que
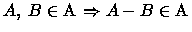 .
.
Definição 1.2.7
Seja

uma
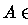
-álgebra em
X. Uma
função
definida em

![$\mu:
\boldsymbol{ \mathscr{A} } \mapsto [0,+\infty]$](img86.gif)
é uma medida se para toda
família
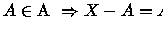
de conjuntos disjuntos vale
Nesta linguagem
 é uma
é uma 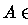 -álgebra em
-álgebra em
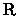 (pelo teorema 1.2.2 )
e
(pelo teorema 1.2.2 )
e
![$\mathfrak{m} :\boldsymbol{ \boldsymbol{ \mathscr{M} } }(\mathbb{R} ^n)\to
[0,+\infty]$](img89.gif) é uma medida (pelo teorema 1.2.3 ).
Outra
é uma medida (pelo teorema 1.2.3 ).
Outra 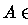 -álgebra fundamental é a
-álgebra fundamental é a 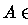 -álgebra de Borel. Para defini-la introduzimos primeiro
o conceito de
-álgebra de Borel. Para defini-la introduzimos primeiro
o conceito de 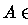 -álgebra gerada por uma família de subconjuntos. Dada uma
família
-álgebra gerada por uma família de subconjuntos. Dada uma
família
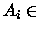 de subconjuntos de X, dizemos que
de subconjuntos de X, dizemos que
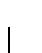 é a
é a 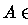 -álgebra
gerada por
-álgebra
gerada por
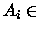 se é a menor
se é a menor 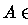 -álgebra que contém
-álgebra que contém
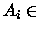 ; mais precisamente, se
; mais precisamente, se
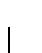 é uma
é uma 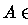 -álgebra e
-álgebra e
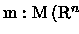 para toda
para toda 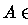 -álgebra
-álgebra
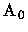 tal que
tal que
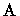 .
Que
.
Que
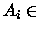 existe é trivial( basta tomar a interseção de todas as
existe é trivial( basta tomar a interseção de todas as
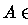 -álgebras em X que contém
-álgebras em X que contém
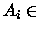 )
e a unicidade segue da
própria
definição.
)
e a unicidade segue da
própria
definição.
Definição 1.2.8
Definimos a
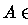
-álgebra de Borel de
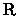
,
e denotamos por
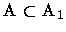
,
como aquela gerada pelos conjuntos fechados.
Como
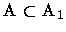 é uma
é uma 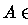 -álgebra , ela contém todos os complementares dos
fechados, isto é, os abertos. Observamos que a
-álgebra , ela contém todos os complementares dos
fechados, isto é, os abertos. Observamos que a 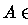 -álgebra gerada pelos abertos
também é a de Borel, porque contém todos os complementares de abertos,
isto é os fechados. Então, denotando-a por
-álgebra gerada pelos abertos
também é a de Borel, porque contém todos os complementares de abertos,
isto é os fechados. Então, denotando-a por
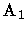 ,
resulta da
definição de
,
resulta da
definição de 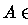 -álgebra gerada por, que
-álgebra gerada por, que
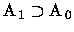 .
Além disso
.
Além disso
porque
 é uma
é uma 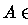 -álgebra que contém todos os
fechados, e estes geram
-álgebra que contém todos os
fechados, e estes geram
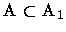 .
.
A relação "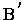 " acima é estrita ( o que demonstraremos
mais tarde), mas todo mensurável é uma união disjunta de um boreleano
e um conjunto de medida zero.
" acima é estrita ( o que demonstraremos
mais tarde), mas todo mensurável é uma união disjunta de um boreleano
e um conjunto de medida zero.
![\begin{proof}% latex2html id marker 566
[Prova do teorema~\ref{T:med.algp}]. Pra...
...i^{'}$\space est\~ao em
$\boldsymbol{ \mathscr{M} }(\mathbb{R} ^n).$\end{proof}](img100.gif)
![\begin{proof}% latex2html id marker 718
[Prova do teorema~\ref{T:med.adtp}.] Pri...
...N$\space fazendo $N\to \infty$\space \ref{E:med.ine} est\'a
provado.
\end{proof}](img101.gif)



Next: Propriedades da medida de
Up: Medida de Lebesgue em
Previous: Introdução
Aldrovando Azeredo Araujo
1998-03-19
 de retângulos tais que
de retângulos tais que
 onde
onde
 .
Decorre do corolário que m* é aditiva
sobre pares de conjuntos disjuntos se um deles é aberto ou fechado. Daremos
agora um exemplo de conjuntos disjuntos para os quais não vale a aditividade
da medida exterior de Lebesgue:
.
Decorre do corolário que m* é aditiva
sobre pares de conjuntos disjuntos se um deles é aberto ou fechado. Daremos
agora um exemplo de conjuntos disjuntos para os quais não vale a aditividade
da medida exterior de Lebesgue:
 .
Observe que T é uma bijeção . Uma órbita de T é um conjunto da
forma
.
Observe que T é uma bijeção . Uma órbita de T é um conjunto da
forma
![]()
![]() .
.
![]() então
x=Tj(y)=Ti(z) with
então
x=Tj(y)=Ti(z) with
![]() .
Mas então
y=T-j(x) and
z=T-i(x). Suponhamos sem perda de generalidade que x>y. Então
existe
.
Mas então
y=T-j(x) and
z=T-i(x). Suponhamos sem perda de generalidade que x>y. Então
existe
![]() tal que i=j+k. Segue que
tal que i=j+k. Segue que
![]() ,
o que é uma
contradição.
,
o que é uma
contradição.
![]()
![]() .
Então, x pertence a alguma órbita de T.
Seja
.
Então, x pertence a alguma órbita de T.
Seja
![]() o elemento de A) nesta órbita. Então existe
o elemento de A) nesta órbita. Então existe
![]() tal que
x=Tk(x0), isto é
tal que
x=Tk(x0), isto é

![]() .
E para estes intervalos vale
que
.
E para estes intervalos vale
que
![]() .
.
![]() fosse válida para quaisquer
fosse válida para quaisquer
![]() disjuntos, então fazendo
Aj=Tj(A0) teríamos
disjuntos, então fazendo
Aj=Tj(A0) teríamos
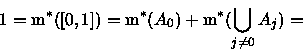
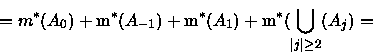
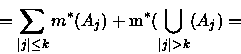
![]() ,
isto é ,
,
isto é ,
![]() .
Mas, neste caso,
.
Mas, neste caso,
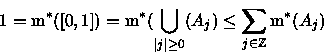
 .
O objetivo natural seria encontrar
uma família de subconjuntos de
.
O objetivo natural seria encontrar
uma família de subconjuntos de
![]()
![\begin{proof}% latex2html id marker 296
[Prova do teorema~\ref{T:med.bpem}.]
(a...
...l}(Q_i)
\end{displaymath}\noindent como quer\'\i amos demonstrar.\\
\end{proof}](img66.gif)
![\begin{proof}% latex2html id marker 382
[Prova do Corol\'ario~\ref{C:med.tecn}]....
...\infty A_n$\space \ e usando a defini\c c\~ao dos $A_n$ 's
temos que
\end{proof}](img67.gif)
![]() para a qual a medida
exterior seja aditiva.
Para tal introduzimos as seguintes definições estabelecidas essencialmente
por Caratheodory.
para a qual a medida
exterior seja aditiva.
Para tal introduzimos as seguintes definições estabelecidas essencialmente
por Caratheodory. separa o par
separa o par
 e
e
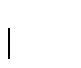 e se,
e se,
![]() ,
sua medida
exterior de Lebesgue denota-se m(A) e se
denomina medida de Lebesgue de A. A família
,
sua medida
exterior de Lebesgue denota-se m(A) e se
denomina medida de Lebesgue de A. A família
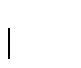 e a função
e a função
![]() são casos particulares do
contexto mais geral dado pelas seguintes definições:
são casos particulares do
contexto mais geral dado pelas seguintes definições: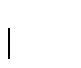 é uma
é uma 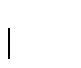 é uma
é uma ![]() -álgebra que contém todos os
fechados, e estes geram
-álgebra que contém todos os
fechados, e estes geram
![]() .
.
![]() " acima é estrita ( o que demonstraremos
mais tarde), mas todo mensurável é uma união disjunta de um boreleano
e um conjunto de medida zero.
" acima é estrita ( o que demonstraremos
mais tarde), mas todo mensurável é uma união disjunta de um boreleano
e um conjunto de medida zero.
![]()
![]()