


Next: Exemplos
Up: Medida Exterior e Medidas
Previous: Introdução
Seja X um conjunto. Denotamos por
 a família de todos os subconjuntos de X.
a família de todos os subconjuntos de X.
Definição 2.2.1
Uma
medida exterior sobre o espço
X é uma função
![$\mu^*:\boldsymbol{ \mathscr{S}}(X)\mapsto [0, +\infty]$](img103.gif)
tal que
- 1.
-

- 2.
-

Se além disto  satisfizer
satisfizer
- 3.
-

dizemos que

é uma medida exterior métrica.
Motivados pela definição de conjunto Lebesgue mensurável estabelecemos a
seguinte definição de conjunto  -mensurável:
-mensurável:
Definição 2.2.2
Dizemos que

é

-mensurável se
para todo par
(
A1,
A2) separado por
A, isto é

,
e

para
i=1,2
Denotamos por
 a família dos
conjuntos
a família dos
conjuntos
 -mensuráveis.
-mensuráveis.
A prova deste teorema é uma repetição das provas do
teorema 1.2.2 e do teorema 1.2.3, trocando-se
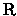 por X e
por X e
 por
por  .
No caso de X ser um espaço
métrico, ainda resta a questão de se saber se todo fechado está em
.
No caso de X ser um espaço
métrico, ainda resta a questão de se saber se todo fechado está em
 .
Caso seja verdade, repetindo-se os
argumentos da seção anterior, obteríamos que
.
Caso seja verdade, repetindo-se os
argumentos da seção anterior, obteríamos que
 conteria a
conteria a 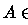 -álgebra dos Boreleanos de X,
denotada por
-álgebra dos Boreleanos de X,
denotada por
 ,
e definida (como no caso de
,
e definida (como no caso de
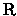 )
como a
)
como a 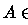 -álgebra gerada pelos conjuntos fechados (ou equivalentemente, pelos abertos).
A resposta a esta questão é fornecida pelo seguinte teorema.
-álgebra gerada pelos conjuntos fechados (ou equivalentemente, pelos abertos).
A resposta a esta questão é fornecida pelo seguinte teorema.
Teorema 2.2.2
Seja
X um espaço métrico e

uma medida exterior sobre
X.
Então

tais que
d(
A,
B)>0.

Definição 2.2.3
Uma uma medida sobre
os boreleanos de
X
![$\mu:\boldsymbol{ \mathscr{B} }(X)\mapsto [0,+\infty]$](img118.gif)
que satisfaz
denomina-se de uma
probabilidade de Borel.



Next: Exemplos
Up: Medida Exterior e Medidas
Previous: Introdução
Aldrovando Azeredo Araujo
1998-03-19
![$\mu^*:\boldsymbol{ \mathscr{S}}(X)\mapsto [0, +\infty]$](img103.gif) tal que
tal que


 satisfizer
satisfizer

![$\mu^*:\boldsymbol{ \mathscr{S}}(X)\mapsto [0, +\infty]$](img103.gif) tal que
tal que

![]() satisfizer
satisfizer
![]() por X e
por X e
![]() por
por ![]() .
No caso de X ser um espaço
métrico, ainda resta a questão de se saber se todo fechado está em
.
No caso de X ser um espaço
métrico, ainda resta a questão de se saber se todo fechado está em
![]() .
Caso seja verdade, repetindo-se os
argumentos da seção anterior, obteríamos que
.
Caso seja verdade, repetindo-se os
argumentos da seção anterior, obteríamos que
![]() conteria a
conteria a ![]() -álgebra dos Boreleanos de X,
denotada por
-álgebra dos Boreleanos de X,
denotada por
 ,
e definida (como no caso de
,
e definida (como no caso de
![]() )
como a
)
como a ![]() -álgebra gerada pelos conjuntos fechados (ou equivalentemente, pelos abertos).
A resposta a esta questão é fornecida pelo seguinte teorema.
-álgebra gerada pelos conjuntos fechados (ou equivalentemente, pelos abertos).
A resposta a esta questão é fornecida pelo seguinte teorema.