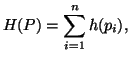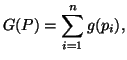Sharma and Taneja (1975) [92] presented an axiomatic characterization of degree
Sharma and Taneja (1975) [92] presented
an axiomatic characterization of degree ![]() .
It is as follows:
.
It is as follows:
Let ![]()
![]() be a real valued function satisfying
be a real valued function satisfying
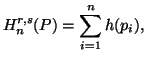
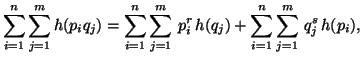 |
(3.17) |
where ![]() be a continuous function with
be a continuous function with![]() .
Then
.
Then
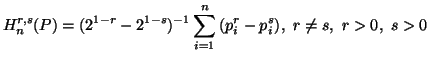 |
(3.18) |
Sharma and Taneja (1977) [93] extended the functional equation (3.17) by the following generalized additivity: