Next:Entropy
of Order andUp:Characterizations
of Generalized Entropies
Previous:Entropy
of Degree Go to:Table
of Contents
Entropy of Kind t
To obtain an entropy of kind t, Arimoto (1971) [3]
used a different approach. Let 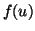 be a real valued scalar function defined and nonnegative on (0,1] with
a continuous derivative on (0,1] and
be a real valued scalar function defined and nonnegative on (0,1] with
a continuous derivative on (0,1] and 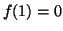 .
For all
.
For all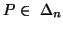 ,
let us define
,
let us define
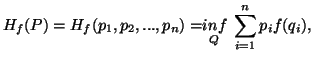
|
|
|
(3.19) |
where the inf. is taken over all probability distributions such
that 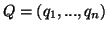 ,
, 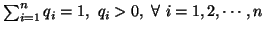 .
.
The function 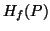 given by (3.19) satisfy some interesting properties (ref. Arimoto, 1971)
[3]. These are summarized in the following
property.
given by (3.19) satisfy some interesting properties (ref. Arimoto, 1971)
[3]. These are summarized in the following
property.
Property 3.24. We have
-
(i)
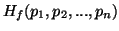 is a continuous and symmetric function with respect to its arguments
is a continuous and symmetric function with respect to its arguments 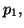
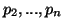 .
.
-
(ii)
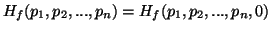 .
.
-
(iii)
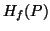 is a concave function with respect to
is a concave function with respect to 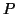 in
in 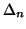 .
.
-
(iv)
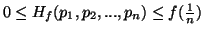 .
.
-
(v) If
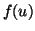 is convex, then
is convex, then
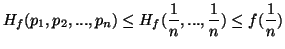
-
(vi) In general
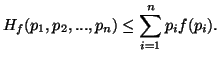
-
(vii) If
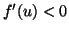 on (0,1), then (a)
on (0,1), then (a) 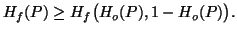 (b)
(b) 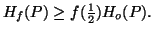
-
(viii) If
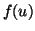 is convex with
is convex with 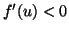 on (0,1], then
on (0,1], then
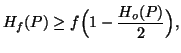 where
where  .
.
Let
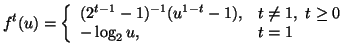 then from (3.19), one has
then from (3.19), one has
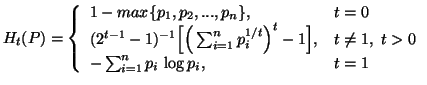
The function 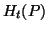 is the entropy of kind
is the entropy of kind 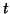 .
It arises as a particular case of (3.19). Some other examples of (3.19)
can be seen in Arimoto (1971) [3]. Boeeke
et al. (1980) [16] studied extensively the
entropy of kind
.
It arises as a particular case of (3.19). Some other examples of (3.19)
can be seen in Arimoto (1971) [3]. Boeeke
et al. (1980) [16] studied extensively the
entropy of kind 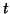 by naming
by naming 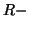 norm,
considering
norm,
considering 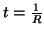 .
Some properties due to Behara and Chawla (1974) [9]
are also worth emphasizing. Following Rényi's approach, the measure
.
Some properties due to Behara and Chawla (1974) [9]
are also worth emphasizing. Following Rényi's approach, the measure 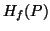 can be characterized. It is not specified here, because the next section
cover it as a particular case.
can be characterized. It is not specified here, because the next section
cover it as a particular case.
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
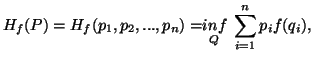
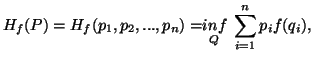
![]() given by (3.19) satisfy some interesting properties (ref. Arimoto, 1971)
[3]. These are summarized in the following
property.
given by (3.19) satisfy some interesting properties (ref. Arimoto, 1971)
[3]. These are summarized in the following
property.
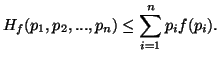
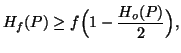
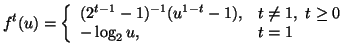
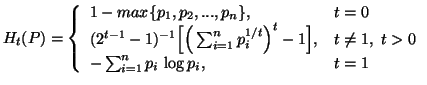
![]() is the entropy of kind
is the entropy of kind ![]() .
It arises as a particular case of (3.19). Some other examples of (3.19)
can be seen in Arimoto (1971) [3]. Boeeke
et al. (1980) [16] studied extensively the
entropy of kind
.
It arises as a particular case of (3.19). Some other examples of (3.19)
can be seen in Arimoto (1971) [3]. Boeeke
et al. (1980) [16] studied extensively the
entropy of kind ![]() by naming
by naming ![]() norm,
considering
norm,
considering ![]() .
Some properties due to Behara and Chawla (1974) [9]
are also worth emphasizing. Following Rényi's approach, the measure
.
Some properties due to Behara and Chawla (1974) [9]
are also worth emphasizing. Following Rényi's approach, the measure ![]() can be characterized. It is not specified here, because the next section
cover it as a particular case.
can be characterized. It is not specified here, because the next section
cover it as a particular case.