Go to:Table of Contents

Unified (r,s)-Relative Information

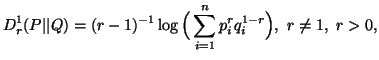
Rényi (1961) [82] first presented a scalar parametric generalization of Kullback-Leibler's relative information as

$$D^1_r(P\vert\vert Q)=(r-1)^{-1}\log\Big(\sum_{i=1}^n{p^r_iq^{1-r}_i}\Big),\r\neq 1,\ r>0,$$ for all $P,Q\ \in\ \Delta_n$, with  $$\lim_{r\to1}{D^1_r(P\vert\vert Q)}=D(P\vert\vert Q).$$

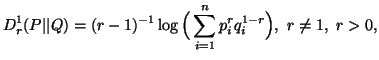
Rathie and Kannappan (1972) [79] presented an alternative way to generalize Kullback-Leibler's information as

$$D^s_s(P\vert\vert Q)=(1-2^{1-s})^{-1}\Big[\sum_{i=1}^n{p^s_iq^{1-s}_i}-1\Big],\s\neq 1,\ s>0,$$ for all $P,Q\ \in\ \Delta_n$, with  $$\lim_{s\to1}{D^s_s(P\vert\vert Q)}=D(P\vert\vert Q).$$

Sharma and Mittal (1977) [91] studied one and two scalar parametric generalizations of $D(P\vert\vert Q)$ as

$$D^s_1(P\vert\vert Q)=(1-2^{1-s})^{-1}\big\{\exp_2\big[(s-1)D(P\vert\vert Q)\big]-1\big\},\s\neq 1,$$ and $$D^s_r(P\vert\vert Q)=(1-2^{1-s})^{-1}\Big[\Big(\sum_{i=1}^n{p^r_iq^{1-r}_i}\Big)^{s-1\overr-1}-1\Big],\ r\neq 1,\ s\neq 1,\ r>0,$$ for all $P,Q\ \in\ \Delta_n$, with  $$\lim_{s\to 1}{D^s_r(P\vert\vert Q)}=D^1_r(P\vert\vert Q),$$ $$\lim_{r\to 1}{D^s_r(P\vert\vert Q)}=D^s_1(P\vert\vert Q),$$ $$\lim_{s\to1}{D^s_1(P\vert\vert Q)}=D(P\vert\vert Q),$$ and  $$D^s_r(P\vert\vert Q)=D^s_s(P\vert\vert Q),\ \$$   for$$\ r=s.$$

Instead studying the measures $D(P\vert\vert Q)$,$D^1_r(P\vert\vert Q)$, $D^s_s(P\vert\vert Q)$, $D^s_1(P\vert\vert Q)$ and $D^s_r(P\vert\vert Q)$ separately, one can study them jointly. Let us write these measures in the unified expression as in case of entropy-type in the following way:

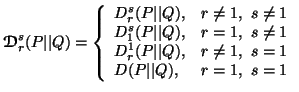$${\ensuremath{\boldsymbol{\mathscr{D}}}}^s_r(P\vert\vert Q)=\left\......rt\vert Q), & r\neq1,\ s=1 \\ D(P\vert\vert Q), & r=1,\ s=1\end{array}\right.$$ (4.1)

for all $P,\ Q\in\Delta_n,\ r\in(0,\infty)$ and $s \in (-\infty,\infty)$.

The measure $D^s_s(P\vert\vert Q)$ does not appear in the unified expression because it is already contained in$D^s_r(P\vert\vert Q)$ as a particular case when $r=s$.

We call the measure ${\ensuremath{\boldsymbol{\mathscr{D}}}}^s_r(P\vert\vert Q)$, the unified $(r,s)-$relative information.

Note 4.1. The definition of $D^s_1(P\vert\vert Q)$ and $D^s_r(P\vert\vert Q)$ given initially by Sharma and Mittal (1977) [91] involve $s>0$. But, here in our study we have relaxed this condition. The constant initially considered was$(2^{s-1}-1)^{-1}\ (s\neq 1)$. Also, we have changed the multiplicative constant and took it as $(1-2^{1-s})^{-1}\ (s\neq1)$ in order to simplify our study on generalized divergence measures. Some study on the measures $D(P\vert\vert Q)$, $D^1_r(P\vert\vert Q)$ and$D^s_s(P\vert\vert Q)$ can be seen in Mathai and Rathie (1975). [71]

In particular, we have

$${\ensuremath{\boldsymbol{\mathscr{D}}}}^s_r(P\vert\vert U)= n^{s-......mbol{\mathscr{H}}}}^s_r(U)-{\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r(P)\big],$$ (4.2)

for all $P=(p_1,p_2,...,p_n)\ \in\ \Delta_n$, $U = ({1\overn},...,{1\over n}) \in \Delta_n$, where ${\ensuremath{\boldsymbol{\mathscr{H}}}}^s_r$ is the unified $(r,s)-$entropy given in Chapter 3, expression (3.8).

As in case of generalized entropies, here also we can write

$${\ensuremath{\boldsymbol{\mathscr{D}}}}^s_r(P\vert\vert Q)={\ensu......cr{N}}}}_s\big({\ensuremath{\boldsymbol{\mathscr{D}}}}^1_r(P\vert\vert Q)\big),$$ (4.3)

where ${\ensuremath{\boldsymbol{\mathscr{N}}}}_s:[0,\infty)\ \rightarrow I\!\!R$ (reals) is given by

$${\ensuremath{\boldsymbol{\mathscr{N}}}}_s(x)=\left\{\begin{array}......(1-2^{1-s})^{-1}\big[2^{(s-1)x}-1\big], & s\neq 1\\ x, & s=1\end{array}\right.$$ (4.4)

Proposition 4.1. The measure ${\ensuremath{\boldsymbol{\mathscr{N}}}}_s(x)$ given by (4.4) has the following properties.

(i) ${\ensuremath{\boldsymbol{\mathscr{N}}}}_s(x)\geq 0$ with equality iff $x=0$;

(ii) ${\ensuremath{\boldsymbol{\mathscr{N}}}}_s(x)$ is an increasing function of x;

(iii) ${\ensuremath{\boldsymbol{\mathscr{N}}}}_s(x)$ is an increasing function of s;

(iv) ${\ensuremath{\boldsymbol{\mathscr{N}}}}_s(x)$ is strictly convex function of x for $s>1$;

(v) ${\ensuremath{\boldsymbol{\mathscr{N}}}}_s(x)$ is strictly concave function of x for $s<1$.