Property 4.1. (Continuity).![]() is a continuous function of the pair
is a continuous function of the pair ![]() and is also continuous with respect to the parameters
and is also continuous with respect to the parameters ![]() and
and ![]() .
.
Property 4.2. (Symmetry).![]() is a symmetric function of their arguments in the pair
is a symmetric function of their arguments in the pair ![]() ,
i.e.,
,
i.e.,
where ![]() is an arbitrary permutation of
is an arbitrary permutation of ![]() to
to ![]() .
.
Property 4.3. (Expansibility). We can write
![]()
Property 4.4.(Nonadditivity). We have
![]()
for all ![]() ,
, ![]() and
and ![]() ,
, ![]() .
.
Property 4.5. (Nonnegativity).![]() with equality iff
with equality iff ![]() .
.
Property 4.6. (Monotonicity).![]() is an increasing function of
is an increasing function of ![]() (
(![]() fixed) and of
fixed) and of![]() (
(![]() fixed). In particular, when
fixed). In particular, when ![]() ,
the result still holds.
,
the result still holds.
Property 4.7. (Inequalities among the measures). We have
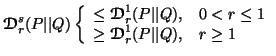
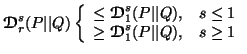
Property 4.9. (Generalized data processing inequality). We have
![]()
where ![]() and
and ![]() are the probability distributions given by
are the probability distributions given by
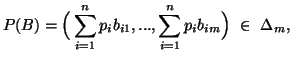
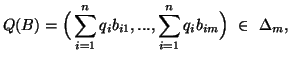
Property 4.10. (Schur-convexity)![]() is a Schur-convex function in the pair
is a Schur-convex function in the pair ![]() .
.
Property 4.11. For ![]() ,
we have
,
we have
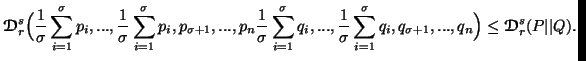
Property 4.12. (Order preserving) We have
![]()
for all ![]() ,
where
,
where ![]() and
and ![]() are determined by the equations:
are determined by the equations:
![]()
![]()