Next:Unified
Divergence MeasuresUp:Generalized
Information Measures
Previous:Unified
Inaccuracies Go to:Table
of Contents
Properties of Unified (r,s)-Inaccuracies
The unified 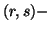 inaccuracy
measures
inaccuracy
measures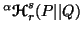
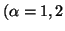 and
and 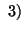 satisfy the following properties:
satisfy the following properties:
Property 4.13. (Continuity)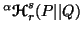
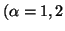 and
and 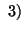 are continuous functions of the pair
are continuous functions of the pair 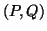 and are also continuous with respect to the parameters
and are also continuous with respect to the parameters 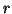 and
and 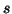 .
.
Property 4.14. (Symmetry)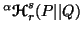
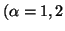 and
and 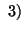 are symmetric function of their arguments in the pair
are symmetric function of their arguments in the pair 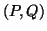 ,
i.e.,
,
i.e.,
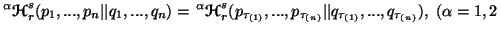 and
and where
where 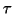 is an arbitrary permutation from
is an arbitrary permutation from 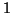 to
to 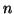 .
.
Property 4.15. (Expansibility) For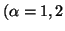 and
and 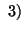 ,
we have
,
we have
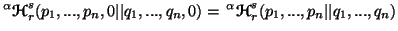
Property 4.16. (Nonadditivity) We have
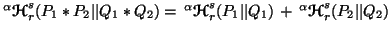
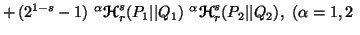 and
and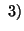 for
for 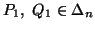 ,
, 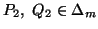 and
and 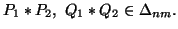
Property 4.17. (Nonnegativity)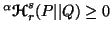
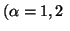 and
and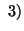 with equality iff
with equality iff 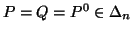 ,
where
,
where 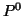 is a distribution such that one of the probabilities is one and all others
are zero.
is a distribution such that one of the probabilities is one and all others
are zero.
Property 4.18. (Monotonicity)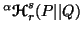
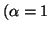 and
and 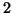 )
are monotonically increasing functions of
)
are monotonically increasing functions of 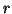 (
(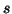 fixed).
fixed).
Property 4.19. We have
-
(i)
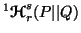 is a convex function of
is a convex function of 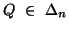 for
for 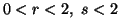 and is concave function of
and is concave function of 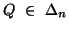 for
for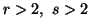 .
.
-
(ii)
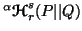
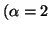 and
and 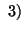 are convex functions of
are convex functions of 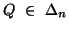 for
for 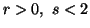 .
.
Property 4.20. (Pseudoconvexity). We have
-
(i)
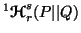 is pseudoconvex function in Q for
is pseudoconvex function in Q for 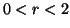 and is pseudoconcave in Q for
and is pseudoconcave in Q for 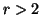 .
.
-
(ii)
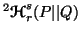 is pseudoconvex in Q for
is pseudoconvex in Q for 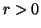 .
.
-
(iii)
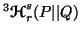 is pseudoconvex in Q for
is pseudoconvex in Q for 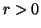 .
.
Note 4.2. It is well known that (ref. Mangasarian, 1969) [68]
every pseudoconvex function is quasiconvex and every pseudoconcave function
is quasiconcave. Thus for the respective values of the parameters 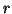 and
and 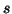 in the above results the quasiconvexity (resp. quasiconcavity) follows.
in the above results the quasiconvexity (resp. quasiconcavity) follows.
Property 4.21. (Schur-convexity) We have
-
(i)
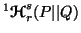 is Schur-convex function in
is Schur-convex function in 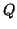 for
for 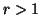 and
is Schur-concave in
and
is Schur-concave in 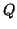 for
for 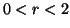 .
.
-
(ii)
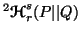 is Schur-convex in
is Schur-convex in 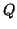 for
for 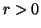 .
.
-
(iii)
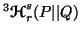 is Schur-convex in
is Schur-convex in 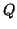 for
for 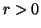 .
.
Property 4.22. (Shannon-Gibbs-type inequalities) We have
-
(i)
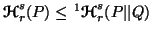 ,
under the following condition:
,
under the following condition:
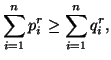
-
(ii)
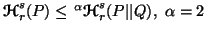 and 3.
and 3.
Note 4.3. The part (i) of the above property can also be proved
under the condition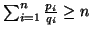 ,
for
,
for 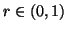 using the techniques similar to Kapur (1987) [54].
using the techniques similar to Kapur (1987) [54].
Property 4.23. (Inequalities among the measures). For 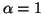 and
and 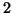 ,
we have
,
we have
-
(i)
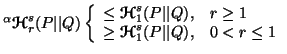
-
(ii)
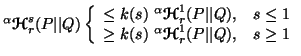
where 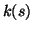 is given by
is given by
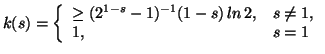
-
(iii)
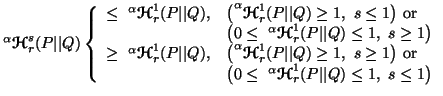 for
for 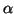 =1 and 2.
=1 and 2.
-
(iv)
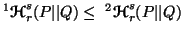 ,
with equality iff either
,
with equality iff either 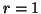 or
or 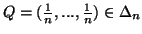 .
.
-
(v)
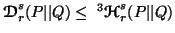 ,
,
-
(vi)
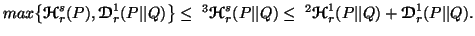
-
(vii)
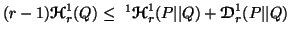 .
.
-
(viii)
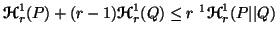 .
.
-
(ix)
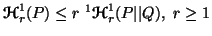 .
.
Note 4.4. The measures 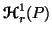 and
and 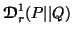 are the one parametric generalizations of the Shannon's entropy and Kullback-Leibler's
directed divergence respectively studied by Rényi (1961) [82].
The measures
are the one parametric generalizations of the Shannon's entropy and Kullback-Leibler's
directed divergence respectively studied by Rényi (1961) [82].
The measures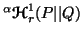 (
(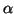 =1,2
and 3) are the three different one parametric generalizations of the Kerridge's
(1961) [63] inaccuracy. The parts (vi) and
(vii) connects these measures in an interesting way. But, unfortunately,
these are not extendable for the unified
=1,2
and 3) are the three different one parametric generalizations of the Kerridge's
(1961) [63] inaccuracy. The parts (vi) and
(vii) connects these measures in an interesting way. But, unfortunately,
these are not extendable for the unified 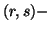 measures.
Moreover, the part (vii) don't have sense for
measures.
Moreover, the part (vii) don't have sense for 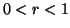 ,
because in this case, the L.H.S. becomes negative. Also for
,
because in this case, the L.H.S. becomes negative. Also for 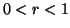 ,
the inequality (viii) have sense, provided the L.H.S. remains positive.
,
the inequality (viii) have sense, provided the L.H.S. remains positive.
Note 4.5. Sharma and Mittal (1977) [91]
and Sharma and Gupta (1976) [89] considered
the properties (3.22) and (3.34) along with other postulates to characterize
the measures 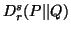 and
and 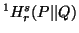 respectively. For a simplified characterization of
respectively. For a simplified characterization of 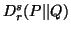 refer to Taneja (1984b) [102].
refer to Taneja (1984b) [102].
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
![]()
![]() and
and ![]() are continuous functions of the pair
are continuous functions of the pair ![]() and are also continuous with respect to the parameters
and are also continuous with respect to the parameters ![]() and
and ![]() .
.
![]()
![]() and
and ![]() are symmetric function of their arguments in the pair
are symmetric function of their arguments in the pair ![]() ,
i.e.,
,
i.e.,
![]() and
and ![]() ,
we have
,
we have
![]()
![]()
![]() and
and![]() with equality iff
with equality iff ![]() ,
where
,
where ![]() is a distribution such that one of the probabilities is one and all others
are zero.
is a distribution such that one of the probabilities is one and all others
are zero.
![]()
![]() and
and ![]() )
are monotonically increasing functions of
)
are monotonically increasing functions of ![]() (
(![]() fixed).
fixed).
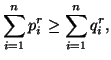
![]() and
and ![]() ,
we have
,
we have
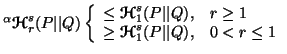
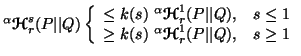
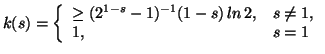
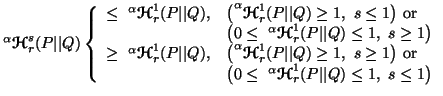 for
for ![]() and
and ![]() respectively. For a simplified characterization of
respectively. For a simplified characterization of ![]() refer to Taneja (1984b) [102].
refer to Taneja (1984b) [102].