Next:Properties
of Unified InaccuraciesUp:Generalized
Information Measures
Previous:Properties
of Unified Relative Go to:Table
of Contents
Unified (r,s)-Inaccuracies
Similar to expression (4.1), we shall give below the three different forms
of writing directly the unified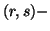 inaccuracy
measures in three different forms:
inaccuracy
measures in three different forms:
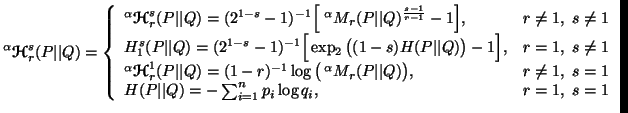
|
|
|
(4.5) |
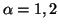 and 3, where
and 3, where
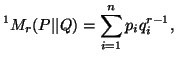
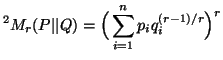
and
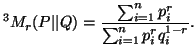
The expressions 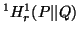 ,
, 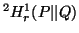 and
and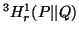 are due to Nath (1968) [73], Van der Lubbe
(1978) [115] and Nath (1975) [74]
respectively. The expressions
are due to Nath (1968) [73], Van der Lubbe
(1978) [115] and Nath (1975) [74]
respectively. The expressions 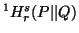 and
and 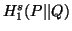 are due to Sharma and Gupta (1976) [89].
are due to Sharma and Gupta (1976) [89].
We can write
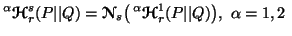 and
and
where 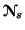 is as given in (4.4).
is as given in (4.4).
From the unified espression (4.5) it is clear that the measures 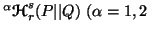 and
and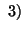 are continuous with respect to the parameters
are continuous with respect to the parameters 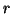 and
and 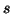 .
This allows us to write
.
This allows us to write
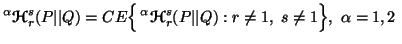 and
and
where "CE" stands for "continuous extension".
In particular, when 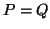 ,
we have
,
we have
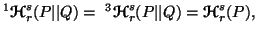
and when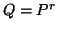 ,
we have
,
we have
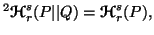 where
where
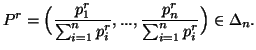
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
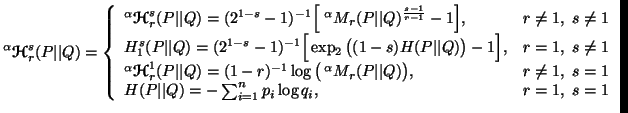
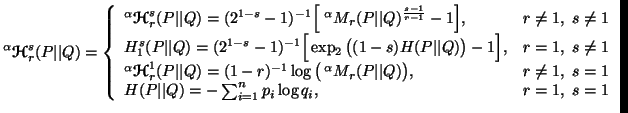
![]() and 3, where
and 3, where
![]() is as given in (4.4).
is as given in (4.4).
![]() and
and![]() are continuous with respect to the parameters
are continuous with respect to the parameters ![]() and
and ![]() .
This allows us to write
.
This allows us to write
![]() and
and![]()
![]() ,
we have
,
we have
![]()