![$\displaystyle ^1{\ensuremath{\boldsymbol{\mathscr{I}}}}^s_r(P\vert\vert Q)= {1\......uremath{\boldsymbol{\mathscr{D}}}}^s_r\big( Q\vert\vert{P+Q\over2}\big)\Bigg],$](img1053.gif) |
(4.6) |
![$\displaystyle ^1{\ensuremath{\boldsymbol{\mathscr{I}}}}^s_r(P\vert\vert Q)= {1\......uremath{\boldsymbol{\mathscr{D}}}}^s_r\big( Q\vert\vert{P+Q\over2}\big)\Bigg],$](img1053.gif) |
(4.6) |
|
|
(4.7) |
The unified ![]() divergence
measures according to the expression (4.6) is given by
divergence
measures according to the expression (4.6) is given by
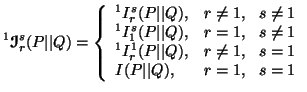
![$ \displaystyle^1I^s_r(P\vert\vert Q)=(1-2^{1-s})^{-1}\Bigg\{ \Big[ \sum_{i=1}^n{p^r_i\Big( {p_i+q_i\over 2}\Big) ^{1-r}}\Big]^{s-1\over r-1}+$](img1056.gif)
![$\displaystyle \Big[\sum_{i=1}^n{q^r_i \Big( {p_i+q_i\over 2}\Big)^{1-r}}\Big]^{s-1\over r-1} -2\Bigg\},\ r\neq 1,\ s\neq 1$](img1057.gif)
![$ \displaystyle^1I^s_1(P\vert\vert Q)=(1-2^{1-s})^{-1}\Big\{ \exp_2\Big[ (s-1)\sum_{i=1}^n{p_i\,\log \Big( {2p_i\over p_i+q_i}\Big)}\Big]+$](img1058.gif)
![$\displaystyle \exp_2\Big[ (s-1)\sum_{i=1}^n{q_i\,\log \Big( {2q_i\overp_i+q_i}\Big)} \Big]-2 \Big\},\ s\neq 1$](img1059.gif)
![$\displaystyle ^1I^1_r(P\vert\vert Q)=\big[ 2(r-1)\big]^{-1}\log\Big\{ \Big[\s......\sum_{i=1}^n{q^r_i \Big( {p_i+q_i\over 2}\Big) ^{1-r}}\Big]\Big\},\ r\neq 1$](img1060.gif)
The unified ![]() divergence
measures according to the expression (4.7) is given by
divergence
measures according to the expression (4.7) is given by
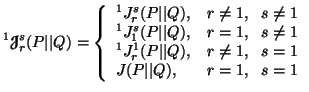
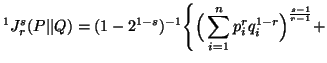
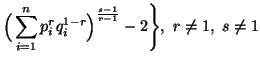
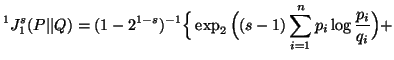
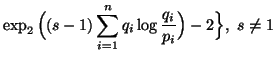
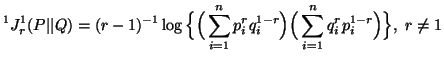
In particular, when ![]() ,
we have
,
we have
![]()
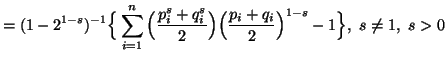 |
(4.8) |
![]()
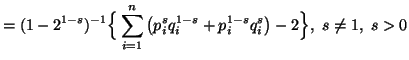 |
(4.9) |
The expressions appearing in (4.8) and (4.9) shall be used to give an
alternative way for generalizing unified ![]() divergence
measures.
divergence
measures.